Полярный момент инерции круга

Для круга вначале вычисляют поляр­ный момент инерции, затем — осевые. Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3).

Площадь каждого кольца можно рас­считать как площадь прямоугольника с длинной стороной, равной длине соответ­ствующей окружности, и высотой, равной толщине кольца:

dA = 2πρ dρ.

Подставим это выражение для площади в формулу для полярного момента инерции: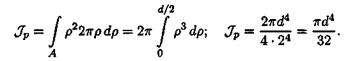

Получим формулу для расчета полярного момента инерции круга: рис. 25.3

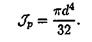
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:

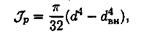
где d — наружный диаметр кольца; d_вн — внутренний диаметр ко­льца.

Если обозначить d_вн /d = с, то

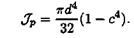
ЛЕКЦИЯ 26