Для ударных волн. Адиабата Гюгонио
Преобразуем полученные уравнения. Уравнение (1) можно представить в виде
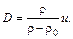 (4)
(4)
Так как при сжатии газа 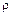 >
> 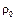 , то из уравнения (4) непосредственно следует, что D и u направлены в одну сторону, причем D < u.
, то из уравнения (4) непосредственно следует, что D и u направлены в одну сторону, причем D < u.
Из уравнения (1) и (2) определяем D и u:
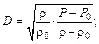 (5)
(5)
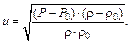 (6)
(6)
Подставляя (5) и (6) после преобразованный получим
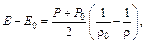
или 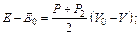 где
где 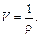
 |
Рисунок 12 – Адиабата Гюгонио для ударной волны
Это уравнение показывает, какие состояния могут получиться из данного начального состояния 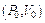 путем однократного сжатия при переходе через фронт ударной волны в плоскости
путем однократного сжатия при переходе через фронт ударной волны в плоскости 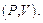 Кривая (АВ) называется адиабатой Гюгонио для ударной волны (рисунок 12).
Кривая (АВ) называется адиабатой Гюгонио для ударной волны (рисунок 12).
2.3 Теория детонационной волны
Когда ударная волна распространяется по ВВ и скорость ее не только больше скорости звука, но и вызывает взрывное разложение ВВ, такую волну называют детонационной.
Явление детонации в газах было открыто в 1881г. независимо Бертло и Вьелем, а также Милляром и Ле-Шателье в ходе работ по исследованию распространения пламени в трубах. Уже первые опыты показали, что после установления стационарного режима детонация распространяется с постоянной скоростью, достигающей для некоторых газовый смесей весьма больших значений порядка 3500–4000 м/с, что в несколько раз больше скорости звука.
Большую роль в развитии теории детонационной волны сыграла гидродинамическая теория детонации. Она дает возможность рассчитать все параметры детонационной волны (скорость, давление, плотность, температуру, энергию).
Основоположником современной гидродинамической теории детонации является русский физик Михельсон (1889г.), также Чепмен (1899г.), Жуге (1905г.) и Крюссар (1907г.).
Согласно гидродинамической теории передача детонации обусловлена распространением по ВВ ударной волны.
Движение обычной ударной волны складывается из движения сначала уплотнения и перемещения самой среды. Распространение детонационной волны обладает более сложной структурой; распространение последней обуславливается движением ударной волны, зоны химической реакции и конечных продуктов взрыва. Поверхность, которая разделяет зону химической реакции и продуктов детонации, называют поверхностью Чепмена-Жуге (например, как на рисунке 7). Исходное ВВ определяется от зоны химической реакции фронтом ударной волны (В-В).
Для описания стационарного процесса детонации достаточно сопоставить состояние исходного вещества и конечных продуктов реакции.
Зона реакции остается неподвижной в системе координат, движущейся со скоростью 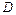 в сторону, противоположную распространению детонации.
в сторону, противоположную распространению детонации.
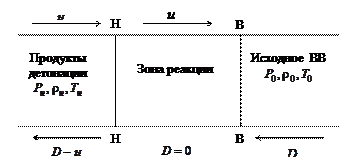 |
Рисунок 13 – Поверхность Чепмена-Жуге
Для определения параметров детонационной волны мы можем воспользоваться основными уравнениями ударных волн.
Введем обозначения:
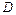 − скорость детонации;
− скорость детонации;
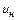 − скорость продуктов реакции за фронтом детонационной волны;
− скорость продуктов реакции за фронтом детонационной волны;
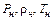 − параметры состояния за зоной химической реакции;
− параметры состояния за зоной химической реакции;
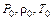 − параметры состояния перед зоной химической реакции;
− параметры состояния перед зоной химической реакции;
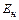 - удельная энергия продуктов за зоной химической реакции;
- удельная энергия продуктов за зоной химической реакции;
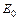 - удельная энергия исходного вещества;
- удельная энергия исходного вещества;
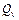 - удельная энергия взрывчатого превращения.
- удельная энергия взрывчатого превращения.
При переходе от ударных волн к детонационным основные уравнения сохранения остаются в силе. Поэтому можно написать:
 (1)
(1)
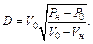 (2)
(2)
Так как для детонационных процессов 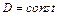 , то последнее уравнение в переменных
, то последнее уравнение в переменных 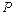 и
и 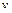 дает прямую линию
дает прямую линию
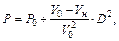 (3)
(3)
проходящую через начальную точку 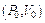 , причем квадрат скорости
, причем квадрат скорости 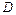 определяется тангенсом угла наклона этой прямой к оси абсцисс. Прямая эта известна под названием прямой Михельсона.
определяется тангенсом угла наклона этой прямой к оси абсцисс. Прямая эта известна под названием прямой Михельсона.
Уравнение Гюгонио принимает следующий вид:
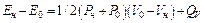 , (4)
, (4)
где 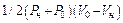 − изменение внутренней энергии вследствие сжатия вещества ударной волной;
− изменение внутренней энергии вследствие сжатия вещества ударной волной;
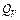 − избыток энергии за счет теплоты реакции.
− избыток энергии за счет теплоты реакции.

B1
Рисунок 14 – Кривая Гюгонио для детонационной волны
Кривая Гюгонио для детонационной волны (АС) построена для конечных продуктов реакции, обладающих повышенным содержанием энергии и поэтому лежит выше кривой Гюгонио для ударной волны.
Для процессов детонации реальное значение имеет лишь ветвь (CH) на кривой Гюгонио, так как вдоль этой ветви, как следует из уравнения (1) и (2) 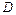 > 0 и
> 0 и 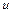 > 0. Ветвь DE, где
> 0. Ветвь DE, где 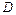 > 0 и
> 0 и 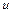 > 0, соответствует процессам горения. Причем продукты горения направлены в сторону противоположную направлению распространения фронта пламени. Участок MD не отвечает никакому реальному стационарному процессу.
> 0, соответствует процессам горения. Причем продукты горения направлены в сторону противоположную направлению распространения фронта пламени. Участок MD не отвечает никакому реальному стационарному процессу.
Проведем из точки A 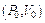 прямую AC под некоторым углом α. Она пересечет кривую Гюгонио в двух точках. Но при этом из условия
прямую AC под некоторым углом α. Она пересечет кривую Гюгонио в двух точках. Но при этом из условия 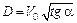 вытекает, что одна и та же скорость детонации может быть реализована при двух различных состояниях разложившегося вещества во фронте волны, что является абсурдом с физической точки зрения.
вытекает, что одна и та же скорость детонации может быть реализована при двух различных состояниях разложившегося вещества во фронте волны, что является абсурдом с физической точки зрения.
Чепмен и Жуге обосновали следующее:
«Процессу детонации отвечает лишь одно единственное состояние продуктов взрыва, характеризуемое точной энтальпией, в которой прямая Михельсона касается адиабаты Гюгонио для продуктов детонации. В этой точке 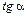 , а следовательно и скорость детонации, достигают своего минимального значения. Эта минимальная стационарная скорость называется нормальной скоростью детонации».
, а следовательно и скорость детонации, достигают своего минимального значения. Эта минимальная стационарная скорость называется нормальной скоростью детонации».
2.4 Механизм распространения детонации по
конденсированным взрывчатым веществам
Гидродинамическая теория детонации для газов применима и к конденсированным ВВ. Фронт детонационной волны также представляет собой ударную волну, в которой ВВ сжимается. При сжатии поглощается энергия, которая компенсируется энергией, выделяющейся в результате химической реакции. Таким образом, интенсивность ударной волны поддерживается, и её должно быть достаточно, чтобы вызвать детонацию в соседнем слое. Однако, ввиду малой сжимаемости конденсированных ВВ разогрев достаточный для достижения скорости реакции, может возникнуть только при скорости детонации порядка
6 – 8 км/с.
В случае ВВ, детонирующих с меньшей скоростью, разогрев за счет гомогенного сжатия становится недостаточным для того, чтобы реакция разложения имела большую скорость.
По А.Я. Апину детонация порошкообразных ВВ представляет собой своеобразное «взрывное горение» отдельных частиц ВВ. Эти частицы воспламеняются в результате адиабатного сжатия газовых включений или струями горячих продуктов взрыва. Нагрев и воспламенение могут осуществляться также при трении частиц друг о друга при сжатии их во фронте детонационной волны.
3 коллоквиум
2.5 Опытное определение скорости детонации
2.5.1 Метод Дотриша
Скорость детонации определяют с помощью специальных приборов – хронографов, причем существует несколько различных методов. Наиболее точным из них является метод детонирующего шнура (метод Дотриша).
Сущность метода в том, что неизвестная скорость детонации заряда сравнивается с известной скоростью детонации детонирующего шнура.
 |
 | |||||
 | |||||
 |
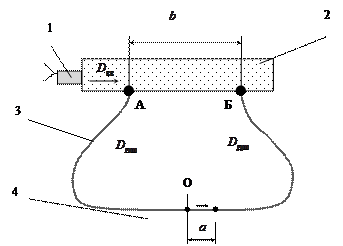
1 – электродетонатор (или капсюль-детонатор); 2 – заряд ВВ;
3 – отрезок детонирующего шнура; 4 – свинцовая пластина
О – середина отрезка шнура; В – метка на пластинке после взрыва
Рисунок 15 – Схема определения скорости детонации по Дотришу
Расстояние между концами шнура является базой для определения скорости детонации и должно быть точно измерено. В левом конце шнура детонация начинается раньше, чем в правом, поэтому место столкновения волн сдвинется вправо и будет находится в точке В, где находится метка от взрыва. В точке О середина шнура. Расстояние между точками О и В обозначим через  Очевидно, что время распространения детонации по левой части шнура
Очевидно, что время распространения детонации по левой части шнура 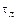 до момента столкновения равно времени распространения детонации по заряду
до момента столкновения равно времени распространения детонации по заряду 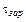 на длине
на длине 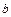 плюс время распространения детонации по правой части шнура
плюс время распространения детонации по правой части шнура 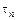 до места столкновения:
до места столкновения:
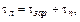 (1)
(1)
где 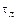 – время распространения детонации по левой части шнура;
– время распространения детонации по левой части шнура;
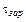 – время распространения детонации по заряду;
– время распространения детонации по заряду;
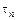 – время распространения детонации по правой части шнура.
– время распространения детонации по правой части шнура.
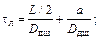 (2)
(2)
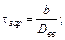 (3)
(3)
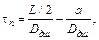 (4) где
(4) где  – длина шнура;
– длина шнура;
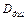 – скорость детонации шнура;
– скорость детонации шнура;
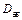 – скорость детонации заряда.
– скорость детонации заряда.
Поскольку
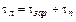
получим
 , (5)
, (5)
откуда
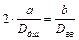 , (6)
, (6)
или
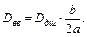 (7)
(7)
Для этого метода достаточно знать 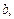
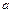 и
и 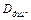 Скорость детонации шнура можно определить фотографическим методом или осциллографическим методом. При определении скорости детонации обычно используют заряды общей длиной 30 – 40 см с длиной базы
Скорость детонации шнура можно определить фотографическим методом или осциллографическим методом. При определении скорости детонации обычно используют заряды общей длиной 30 – 40 см с длиной базы
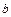 = 20 - 25 см. При этих условиях ошибка однократного измерения составляет 3 – 5 %.
= 20 - 25 см. При этих условиях ошибка однократного измерения составляет 3 – 5 %.
2.5.2 Фотографический метод
Для фотографирования применяются приборы, называемые фоторегистрами. Существует два типа фоторегистров:
- фоторегистры с барабанной разверткой;
- фоторегистры с зеркальной разверткой.
Дата добавления: 2015-08-08; просмотров: 3447;
