Декартово произведение. Определение. Декартовым произведением двух отношений R1 (R11, R12, ,R1n), R2,(R21, R22, ,R2m) называется отношение
Определение. Декартовым произведением двух отношений R1 (R11, R12, …,R1n), R2,(R21, R22, …,R2m) называется отношение, заголовок которого является сцеплением заголовков отношений R1 и R2:
(R11, R12, …,R1n ,R21, R22, …,R2m),
а тело состоит из кортежей, являющихся сцеплением кортежей отношений R1 и R2:
(r11, r12, …,r1n ,r21, r22, …,r2m),
таких, что:
(r11, r12, …,r1n) 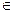 R1 , (r21, r22, …,r2m)
R1 , (r21, r22, …,r2m) 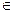 R2,
R2,
При выполнении прямого произведения двух отношений получается отношение, кортежи которого являются конкатенацией (сцеплением) кортежей первого и второго операндов. Синтаксис операции декартового произведения:
R1 times R2
Замечание. Мощность произведения R1 times R2 равна произведению мощностей отношений R1 и R2, т. к. каждый кортеж отношения R1 соединяется с каждым кортежем отношения R2.
Если в отношениях R1 и R2 имеются атрибуты с одинаковыми наименованиями, то перед выполнением операции декартового произведения такие атрибуты необходимо переименовать. При перемножении отношений совместимость по типу не требуется.
Пример. Пусть даны два отношения R1 и R2 с информацией о студентах и дисциплинах (рис. 6.5). Декартово произведение отношений R1 и R2 будет иметь вид, представленный на рис. 6.6.
Отношение R1 (Студенты)
| Личный номер | Фамилия |
| Котова | |
| Серов | |
| Леонидов |
Отношение R2 (Название дисциплины)
| Код дисциплины | Название дисциплины |
| Высшая математика | |
| История | |
| Иностранный язык |
Рис. 6.5. Примеры отношений R1 и R2
Отношение R1 times R2
| Личный номер | Фамилия | Код дисциплины | Название дисциплины |
| Котова | Высшая математика | ||
| Котова | История | ||
| Котова | Иностранный язык | ||
| Серов | Высшая математика | ||
| Серов | История | ||
| Серов | Иностранный язык | ||
| Леонидов | Высшая математика | ||
| Леонидов | История | ||
| Леонидов | Иностранный язык |
Рис. 6.6. Результат операции декартова произведения для отношений R1 и R2
Замечание. Операция декартова произведения непосредственно для реальных запросов не используется, но она важна для выполнения специальных операций [20, С. 55-64].
Дата добавления: 2015-08-08; просмотров: 982;
