ЯДЕРНАЯ СТРУКТУРА АТОМА

Альфа-частицы. В 1896 году французским физиком Беккерелем было открыто явление радиоактивности. После этого начался быстрый прогресс в изучении строения атома. Этому, прежде всего способствовало то, что в руках физиков оказался очень эффективный инструмент исследования атомной структуры – α-частица. С помощью α-частиц, испускаемых естественными радиоактивными веществами, были сделаны важнейшие открытия: установлена ядерная структура атома, получены первые ядерные реакции, обнаружено явление искусственной радиоактивности и, наконец, найден нейтрон, сыгравший важную роль как при объяснении строения атомного ядра, так и при открытии процесса деления тяжелых ядер.

Альфа-частицы – это движущиеся с большой скоростью ядра гелия. Измерения скоростей α-частиц естественных излучателей по отклонению в электрическом и магнитном полях дали величину скорости (1,5-2).10⁷ м/с, что соответствует кинетической энергии 4,5-8 МэВ (1 МэВ=1,6.10^-13 Дж). Такие частицы движутся в веществе прямолинейно, быстро теряют энергию на ионизацию атомов и после остановки превращаются в нейтральные атомы гелия.

Рассеяние альфа-частиц. Опыты Резерфорда. Изучая прохождение коллимированного пучка альфа-частиц через тонкую металлическую фольгу, английский физик Резерфорд обратил внимание на размытие изображения пучка частиц на регистраторе – фотопластинке. Резерфорд объяснил это размытие рассеянием альфа-частиц. Детальное изучение рассеяния альфа-частиц показало, что в редких случаях они рассеиваются на большие углы иногда превышающие 90⁰, что соответствует отбрасыванию быстродвижущихся частиц в обратном направлении. Такие случаи рассеяния в рамках модели Томпсона объяснить нельзя.

Тяжелая альфа-частица в одном акте столкновения может быть отброшена назад только при взаимодействии с частицей большей массы, превосходящей массу альфа-частицы. Электроны не могут быть такими частицами. Кроме того, рассеяние в обратном направлении предполагает сильное торможение альфа-частицы, т.е. энергия взаимодействия должна быть порядка кинетической энергии альфа-частицы. Энергия же электростатического взаимодействия альфа-частицы с атомом Томпсона, имеющим положительный заряд, распределенный в объеме или на поверхности атома радиусом 10^-8 см и равный в единицах элементарного заряда примерно половине атомной массы, много меньше этой величины. Результаты опыта можно объяснить, если расстояние от альфа частицы до центра положительного электрического заряда порядка 10^-12 см. Такое расстояние в 10000 раз меньше радиуса атома, а радиус положительного заряда должен быть еще меньше. Предположение о малом объеме рассеивающего центра согласуется с очень малым количеством случаев рассеяния на большие углы.

Для объяснения результатов своих наблюдений по рассеянию альфа-частиц Резерфорд предложил ядерную модель атома. Согласно этой модели в центре атома находится ядро, занимающее очень малый объем, содержащее почти всю массу атома и несущее положительный электрический заряд. Основной объем атома занят движущимися электронами, число которых равно числу элементарных положительных зарядов ядра, т.к. атом в целом нейтрален.

Теория рассеяния альфа-частиц. Чтобы обосновать предположение о ядерной структуре атома и доказать, что рассеяние альфа-частиц происходит в результате кулоновского взаимодействия с ядром, Резерфорд развил теорию рассеяния альфа-частиц точечными электрическими зарядами с большой массой и получил зависимость между углом рассеяния θ и числом частиц, рассеянных на угол θ. Если альфа-частица движется в направлении точечного заряда Ze, где Z – число элементарных зарядов, и при этом ее начальная траектория отстоит от оси, проходящей через рассеивающий центр, на расстоянии а (рис.1.1), то на основании закона Кулона методами классической механики можно вычислить угол θ, на который отклонится альфа-частица вследствие электростатического отталкивания одноименных электрических зарядов:

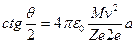, (1.1)

где M и v – масса и скорость альфа-частицы; 2e – ее заряд; ε₀ – электрическая постоянная, равная 8,85.10^-12 Ф/м.

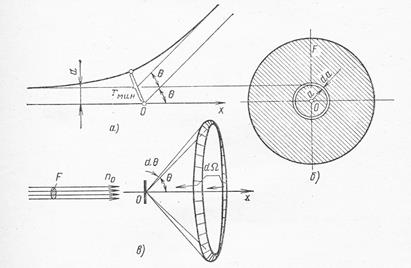
Рис.1.1. Рассеяние альфа-частицы электрическим полем атомного ядра:

а) – схема рассеяния в плоскости траектории частицы; б) – кольцо, из которого происходит рассеяние под углом θ; в) – схема рассеяния в конический телесный угол под угломθ к оси.

Доля частиц dn/n₀, имеющих параметр удара а, от полного числа n₀, падающих на мишень, равна доле элементарной площадки 2πada на полной площади F поперечного сечения пучка альфа-частиц (рис. 1.1, б). Если на площади F имеется не один, а N_F рассеивающих центров, то соответствующая доля возрастет в N_F раз и отнесенная к единице а, составит:

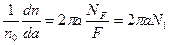, (1.2)

где N₁ – число рассеивающих центров на единице площади мишени.

Учитывая, что dΩ=2π sinθ dθ, можно получить долю частиц, рассеянных в единицу конического телесного угла 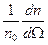под углом θ к оси, как :

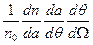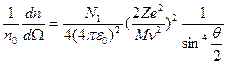(1.3)

Экспериментальная проверка полностью подтвердила последнюю зависимость при рассеянии веществом альфа-частиц. Строгое выполнение закона 1/sin⁴ 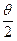свидетельствует о том, что за рассеяние ответственны только электрические силы и что геометрические размеры электрических зарядов обоих тел по крайней мере меньше наименьшего расстояния в акте рассеяния r_мин. Расстояние r_мин тем меньше, чем больше угол рассеяния θ. При θ=π ( 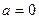) оно самое малое и определяется условием 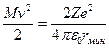, которое соответствует случаю обращения всей кинетической энергии альфа-частицы в потенциальную энергию отталкивания одноименных зарядов.

По результатам обработки результатов экспериментов, исходя из различных в то время оценок величины заряда ядер Z, Резерфорд оценил радиус ядра величиной порядка 10^-12 см.

Атом Резерфорда-Бора. С открытием атомного ядра возникла необходимость объяснения устойчивости атома. С точки зрения классической электродинамики атом Резерфорда не может существовать длительно. Поскольку разноименные заряды притягиваются, электроны могут находится на определенном расстоянии от ядра только при условии движения вокруг ядра. Однако движение по замкнутой траектории является движением с ускорением, а движущийся с ускорением электрический заряд излучает энергию в окружающее пространство. За ничтожно малое время любой атом должен излучить энергию движения электронов и уменьшиться до размера ядра.

Первую стационарную модель атома предложил датский физик Нильс Бор в 1913 году. Бор связал устойчивость атомов с квантовой природой излучения. Гипотеза квантов энергии, выдвинутая немецким физиком Планком в 1900 году для объяснения спектра излучения абсолютно черного тела, утверждала, что микроскопические системы способны излучать энергию лишь определенными порциями – квантами с частотой v, пропорциональной энергии кванта E:

E=hv,

где h – универсальная постоянная Планка, равная 6,62.10^-24 Дж.с.

Бор предположил, что энергия атомного электрона в кулоновском поле ядра не меняется непрерывно, а принимает ряд устойчивых дискретных значений, которым соответствуют стационарные орбиты электронов. При движении по таким орбитам электрон не излучает энергию. Излучение атома происходит только при переходе электрона с орбиты с более высоким значением энергии на другую стационарную орбиту. Это излучение характеризуется единственным значением частоты, пропорциональной разности энергий орбит:

hv=Е_нач - Е_кон

Условие стационарности орбиты – это равенство механического момента количества движения электрона целому кратному числу 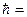h/2π:

mvr_n = n ,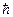

где mv – модуль импульса электрона;

r_n – радиус n-ой стационарной орбиты;

n – любое целое число.

Введенное Бором условие квантования круговых орбит позволило рассчитать спектр атома водорода и вычислить спектроскопическую константу Ридберга для атома водорода. Система уровней одноэлектронного атома и радиусы стационарных орбит можно определить из последнего соотношения и закона Кулона:

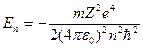; (1.4)

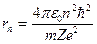. (1.5)

Расчет по этим формулам при n=1 и Z=1 дает радиус наименьшей стационарной орбиты электрона в атоме водорода или первый боровский радиус:

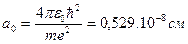. (1.6)

Движение электрона по орбите можно представить как замкнутый электрический ток и вычислить создаваемый им магнитный момент. Для первой орбиты водорода он называется магнетоном Бора и равен:

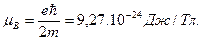(1.7)

Магнитный момент обратно пропорционален массе частицы, но для частиц данного сорта, например электронов, имеет смысл единицы. Характерно, что как раз этой единице равен собственный момент электрона, связанный с его спином.

Ядерная модель атома с электронами на устойчивых орбитах называется планетарной моделью Резерфорда-Бора. Она не приводит к верным количественным результатам в приложении к атомам с более, чем одним электроном, но зато очень удобна при качественной интерпретации атомных явлений. Точную теорию атома дает квантовая механика.

Дискретная природа микромира. Открытие атомного строения вещества оказалось первым шагом на пути открытий дискретной природы микромира. Не только массы и электрические заряды микротел дискретны, но и динамические величины, описывающие состояния микросистем, такие, как энергия, момент количества движения, также дискретны и характеризуются скачкообразным изменением своих численных значений.