Движение в гравитационном поле.

В 1687 г. Ньютон на основании уже обнаруженных к тому времени на опыте законов движения планет установил, что всякие два тела притягиваются друг к другу с силой, прямо пропорциональной квадрату расстояния между ними. Например, материальная точка с массой m, находящаяся на расстоянии r от другой материальной точки с массой M, будет притягиваться последней с силой

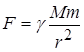, (1.39)

где γ— размерная постоянная, необходимая для того, чтобы величина F имела размерность силы. В случае наличия тел сложной формы, когда их нельзя рассматривать как материальные точки, формула (1.39) видоизменяется, но основной характер взаимодействия сохраняется. Постоянная в уравнении (1.39) была впервые определена в 1798г. английским физиком Кавендишем в поразительном по точности опыте. Ее численное значение очень мало γ = 6.6·lO^-11н·м²/кг² — это значит, что с силой столь малой величины притягиваются друг к другу две массы в 1кг каждая на расстоянии в 1м. Огромное значение, которое имеют силы гравитации в природе, обусловлено с одной стороны, большими массами небесных тел, а с другой — отсутствием сил иного происхождения.

Соотношение (1.39) носит название закона всемирного тяготения. Оно хорошо описывает движение тяготеющих масс.

С физической точки зрения соотношение (1.39) описывает взаимодействие массы m с полем тяготения, или, как принято говорить, с гравитационным полем, создаваемым в пространстве массой M. Хотя способ передачи гравитационного взаимодействия нам неизвестен, опыт показывает, что с каждой массой в пространстве связано гравитационное поле.

Гравитационное поле, создаваемое в пространстве массой M, будем характеризовать потенциалом

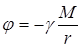. (1.40)

Потенциальная энергия, приобретенная телом с массой в этом поле, согласно результатам предыдущего раздела, может быть записана в виде

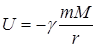, (1.41)

т. е. потенциальная энергия поля в гравитационном поле равна потенциалу поля в точке нахождения тела, умноженному на массу тела.

Сила притяжения (1.39) может быть найдена по формуле (1.35):

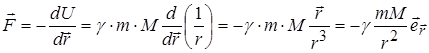(1.42)

( — единичный вектор в направлении радиус-вектора r).

Зная потенциал поля, можно вычислить работу, совершаемую силами поля над телом с массой т при перемещении его из положения 1 в положение 2. Эта работа может быть выражена через разность значений потенциала поля в указанных точках

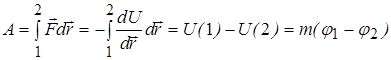(1.43)

Отсюда видно, что работа в поле сил тяготения не зависит от пути, т. е. от того, каким образом тело было перемещено из положения 1 в 2.

Массы, фигурирующие в законе всемирного тяготения, характеризуют способность тел создавать поле тяготения и в свою очередь испытывать на себе их действие. Поэтому масса, о которой идет здесь речь, может быть названа тяготеющей, или гравитационной, массой, в отличие от инертной массы, фигурирующей во втором законе Ньютона. Хотя их физический смысл различен и ниоткуда не следует их равенство, тем не менее они все же тождественны. Невозможность различить обе массы является следствием большого числа самых совершенных опытов. Таким образом, во втором законе Ньютона и в законе тяготения проявляются различные свойства одной и той же величины — физической массы.