Закон взаимосвязи массы и энергии.

Найдем кинетическую энергию релятивистской частицы. Раньше было показано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:

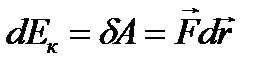(6.1)

Учитывая, что , и подставив в (6.1) выражение (5.2), получаем

.

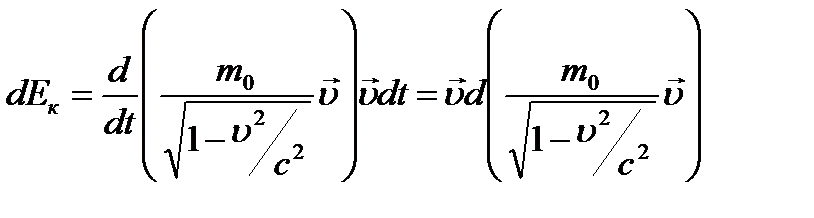Преобразовав данное выражение с учетом того, что 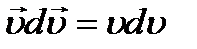, и формулы (6.1), придем к выражению

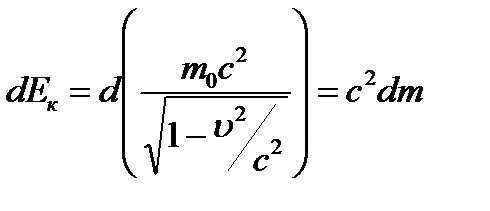, (6.2)

т. е. приращение кинетической энергии частицы пропорционально приращению ее массы.

Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя , то, проинтегрировав (6.2), получим

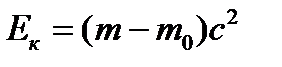, (6.3)

или кинетическая энергия релятивистской частицы имеет вид

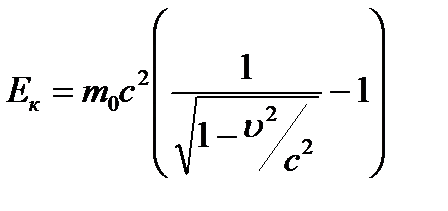. (6.4)

Выражение (6.4) при скоростях 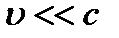переходит в классическое:

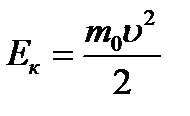
(разлагая в ряд 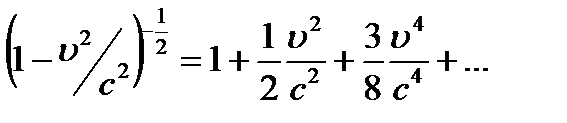при 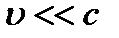, правомерно пренебречь членами второго порядка малости).

А.Эйнштейн обобщил положение (6.2), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии, а именно любое изменение массы 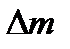сопровождается изменением полной энергии частицы,

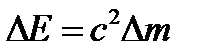. (6.5)

Отсюда А.Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:

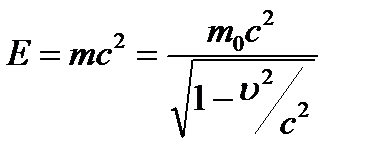. (6.6)

Уравнение (6.6), равно как и (6.5), выражает фундаментальный закон природы – за­кон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. Закон (6.6) можно, учитывая выражение (6.3), записать в виде

,

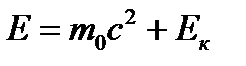откуда следует, что покоящееся тело (Е_к=0) также обладает энергией

,

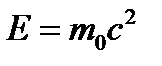называемой энергией покоя.В классической механике энергия покоя Е₀ не учитывается, считая, что при 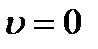энергия покоящегося тела равна нулю.

В силу однородности временив релятивистской механике, как и в классической, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Из формул (6.6) и (5.4) найдем релятивистское соотношение между полной энергией и импульсом частицы:

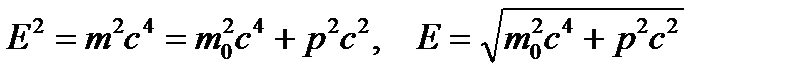. (6.7)

Возвращаясь к уравнению (6.6), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко всем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса

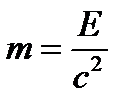(6.8)

и, наоборот, со всякой массой связана энергия (6.6).

Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро – на протоны и нейтроны). Энергия связи системы

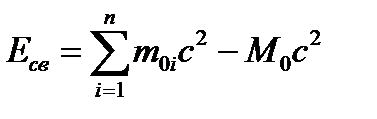. (6.9)

где m_0i – масса покоя i-й частицы в свободном состоянии; М₀ – масса покоя системы, состоящей из п частиц.

Закон взаимосвязи (пропорциональности) массы и энергии блестяще подтвержден экспериментом о выделении энергии при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превращениях элементарных частиц.

Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер; наконец, масса и энергия оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи.

Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи – пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.