Как работает триггер
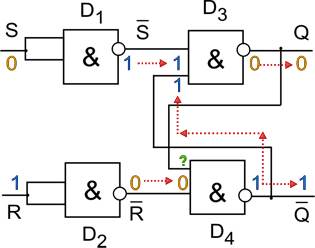 |
Рис. 5.1.а. Логическая схема триггера (R=1, S=0)
1. Пусть на входе R установлена 1, на S - 0. Логические элементы D1 и D2 инвертируют эти сигналы, т.е. меняют их значения на противоположные. В результате на вход элемента D3 поступает 1, а на D4 - 0.
Поскольку на одном из входов D4 есть 0, независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера - ) обязательно установится 1. Эта единица передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0.
Итак, при R=1 и S=0 на прямом выходе триггера устанавливается Q=0, а на инверсном - =1.
Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации выходных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер "устанавливается в 0" или "сбрасывается". Сброс по-английски называется "Reset", отсюда вход, появления сигнала на котором приводит к сбросу триггера, обычно обозначается буквой R.
2. Проводя аналогичные рассуждения для "симметричного" случая R=0 и S=1, получим, что на прямом выходе получится логическая 1 (Q=1), а на инверсном - 0 ( =0).
3. Теперь рассмотрим наиболее распространенную и интересную ситуацию R=0 и S=0 - входных сигналов нет.
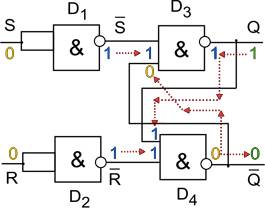
Рис. 5.1.б. Логическая схема триггера
(R=0, S=0, "предыдущие" состояния выходов Q=1, =0)
Тогда на входы элементов D3 и D4, связанные с R и S, будет подана 1 и их выходной сигнал будет зависеть от сигналов на противоположных входах. Нетрудно убедиться, что такое состояние будет устойчивым. Пусть, например, на прямом входе 1. Тогда наличие единицы на обоих входах элемента D4 "подтверждает" нулевой сигнал на его выходе. В свою очередь наличие 0 на инверсном выходе передается на D3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q=0.
Дата добавления: 2015-08-08; просмотров: 1063;
