Давление. Закон Паскаля.

Глава 5. Механика жидкостей и газов.

Гидростатика и аэростатика – разделы механики, которые изучают равновесие жидкостей и газов.

Гидродинамика и аэродинамика – разделы механики, которые изучают движение жидкостей и газов.

Гидростатика (аэростатика).

Давление. Закон Паскаля.

Давление – это скалярная величина, равная отношению нормальной компоненты силы, действующей на элементарную площадку внутри жидкости, к площади этой элементарной площадки.

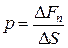. (5.1.1)

Касательные составляющие силы DF не существенны, т.к. приводят к текучести жидкости, т.е. нарушению равновесия.

Единицы давления. В СИ – Па (паскаль): 1 Па = 1 Н/м²;

в СГС – дин/см².

Внесистемные единицы: физическая (нормальная) атмосфера (атм) равна давлению столба ртути высотой 760 мм;

миллиметр ртутного столба (мм. рт. ст.).

1мм. рт. ст. = r_рт.gh = (13,6×10³ кг/м³)×(9,81 м/с²)×(10^-3м) = 133 Па.

1 атм = 760 мм. рт. ст. = 1,01×10⁵ Па.

Свойства покоящейся жидкости (газа).

1. Сила, вызванная давлением покоящейся жидкости, действует всегда перпендикулярно поверхности, с которой эта среда соприкасается.

2. Жидкости и газы создают давление во всех направлениях.

Силы, действующие на частицы жидкости или газа, относятся к одному из двух видов.

1) Объемные силы – это силы дальнодействия, которые действуют на каждый элемент объема жидкости или газа. Примером такой силы служит сила тяжести.

2) Поверхностные силы – это силы близкодействия, которые возникают в результате непосредственного контакта между взаимодействующими элементами жидкости, газа и твердого тела на их общей границе. Примером поверхностной силы является сила атмосферного давления.

Закон Паскаля. Поверхностные силы, действующие на неподвижную жидкость (или газ), создают давление, одинаковое во всех точках жидкости (газа). Величина давления в любой точке жидкости (газа) не зависит от направления (т.е. от ориентации элементарной площадки).

Доказательство.

1. Докажем, что давление в данной точке жидкости одинаково по всем направлениям.

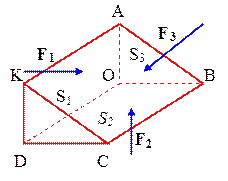
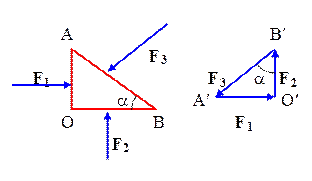
Рис. 5.1.1.а Рис. 5.1.1.б

Для доказательства воспользуемся принципом отвердевания: любой элемент жидкости можно рассматривать как твердое тело и применять к этому элементу условия равновесия твердого тела.

Выделим мысленно в окрестности данной точки жидкости бесконечно малый отвердевший объем в виде трехгранной призмы (рис. 5.1.1), одна из граней которой (грань OBCD) расположена горизонтально. Площади оснований AOB и KDC будем считать малыми, по сравнению с площадями боковых граней. Тогда малым будет объем призмы, а, следовательно, и сила тяжести, действующая на эту призму.

На каждую грань призмы действуют поверхностные силы F₁, F₂ и F₃. Из равновесия жидкости следует, что 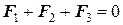, т.е. векторы F₁, F₂ и F₃ образуют треугольник ( 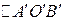на рис. 5.1.1.б), подобный треугольнику . Тогда

.

Умножим знаменатели этих дробей на OD = BC = AK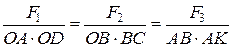, Þ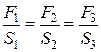

, Þ , Þ .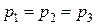

Таким образом, давление в неподвижной жидкости не зависит от ориентации площадки внутри жидкости.

2. Докажем, что давление в двух любых точках жидкости одинаково.

Рис. 5.1.2.

Рассмотрим две произвольные точки A и B жидкости, отстоящие друг от друга на расстояние DL. Выделим в жидкости произвольно ориентированный цилиндр, в центрах оснований которого находятся выбранные нами точки A и B (рис. 5.1.2). Площади оснований цилиндра DS будем считать малыми, тогда объемные силы также будут малыми по сравнению с поверхностными.

Предположим, что давления в точках A и B разные: 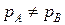, тогда 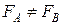, а значит, выделенный объем придет в движение. Полученное противоречие доказывает, что давление в двух любых точках жидкости одинаково.

Примером поверхностных сил, для которых выполняется закон Паскаля, является сила атмосферного давления.

Атмосферное давление – это давление, которое оказывает воздух атмосферы на все тела; оно равно силе тяжести, действующей на столб воздуха с единичной площадью основания.

Опыт Торричелли продемонстрировал наличие атмосферного давления и впервые позволил его измерить. Этот опыт был описан в 1644 году.

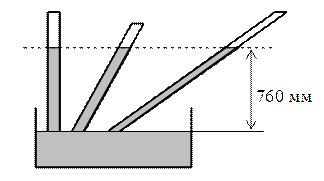
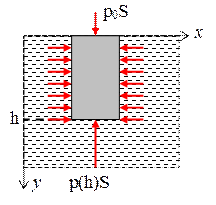
Рис. 5.1.3. Рис. 5.1.4.

В этом опыте длинная стеклянная трубка, запаянная с одного конца, наполняется ртутью; затем открытый конец ее зажимается, после чего трубка перевертывается, опускается зажатым концом в сосуд с ртутью и зажим снимается. Ртуть в трубке при этом несколько опускается, т.е. часть ртути выливается в сосуд. Объем пространства над ртутью в трубке называется торричелевой пустотой. (Давление паров ртути в торричелевой пустоте при 0°C составляет 0,025 Па.)

Уровень ртути в трубке одинаков независимо от того, как установлена трубка: вертикально или под углом к горизонту (рис. 5.1.3). При обычных нормальных условиях вертикальная высота ртути в трубке составляет h = 760 мм. Если бы вместо ртути трубка была заполнена водой, то высота h = 10,3 м.

Приборы, применяемые для измерения атмосферного давления, называются барометрами. Простейший ртутный барометр представляет собой трубку Торричелли.

Для того, чтобы объяснить, почему трубка Торричелли действительно позволяет измерить атмосферное давление, обратимся к рассмотрению объемных сил и вычислению зависимости давления в жидкости от глубины h.

Давление в жидкости, создаваемое объемными силами, т.е. силой тяжести, называется гидростатическим давлением.

Получим формулу для давления жидкости на глубине h. Для этого выделим в жидкости затвердевший параллепипед, одно из оснований которого находится на поверхности жидкости, а другое на глубине h (рис. 5.1.4). На этой глубине на параллепипед действуют силы, изображенные на рисунке.

Силы, действующие на параллепипед, вдоль оси x уравновешены. Запишем условие равновесия сил вдоль оси y.

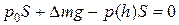, (5.1.2)

где p₀ – атмосферное давление, 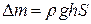- масса параллепипеда, r - плотность жидкости. Тогда

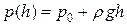, (5.1.3)

Первое слагаемое в формуле (5.1.3) связано с поверхностными силами, а второе слагаемое 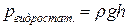, называемое гидростатическим давлением, связано с объемными силами.

Если сосуд с жидкостью движется с ускорением a, направленным вниз, то условие (5.1.2) принимает вид: 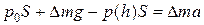, Þ

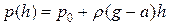. (5.1.4)

В состоянии невесомости (a = g) гидростатическое давление равно нулю.

Примеры применения закона Паскаля.

1. Гидравлический пресс (рис. 5.1.5).

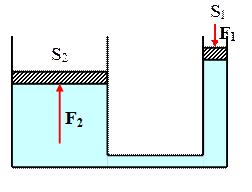
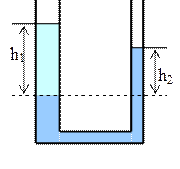
Рис. 5.1.5. Рис. 5.1.6. Рис. 5.1.7.

Если к правому колену гидравлического пресса приложить силу F₁, то из закона Паскаля: p₁ = p₂, следует

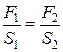, Þ 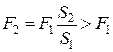, т.к. S₂ > S₁.

С помощью такого пресса, прикладывая к правому поршню силу F₁, с левой стороны получим большую силу F₂. При этом, если правый поршень сместится на L₁, то из условия несжимаемости жидкости: 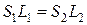, получим, что левый стержень поднялся на .

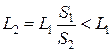Свойство гидравлического пресса: сколько выигрываем в силе, столько проигрываем в расстоянии.

2. Сообщающиеся сосуды.

а) Однородная жидкость в сообщающихся сосудах устанавливается на одном горизонтальном уровне (рис. 5.1.6).

б) Для различных жидкостей (рис. 5.1.7): 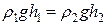, Þ .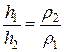

3. Гидростатический парадокс. (рис. 5.1.8).

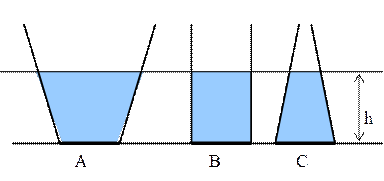
Рис. 5.1.8.

Возьмем три сосуда различной формы, но с одинаковой площадью сечения дна. Предположим эта площадь равна S = 20 см² = 0,002 м². Уровень воды во всех сосудах одинаков и равен h = 0,1 м. Однако из-за различной формы сосудов в них находится разное количество воды. В частности, в сосуде A налита вода весом 3 Н, в сосуде B – весом 2 Н и в сосуде C – весом 1 Н.

Гидростатическое давление на дно во всех сосудах равно 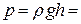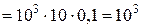Па. Одинакова и сила давления воды на дно сосудов 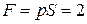Н. Как может вода весом 1 Н в третьем сосуде создать силу давления 2 Н?

Для объяснения гидростатического парадокса следует учесть силы реакции, действующие со стороны стенок (рис. 5.1.9).

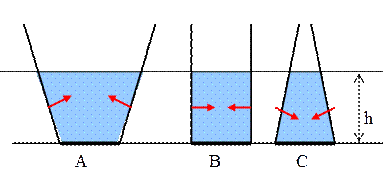
Рис. 5.1.9.