Цепь с параллельными ветвями
 |
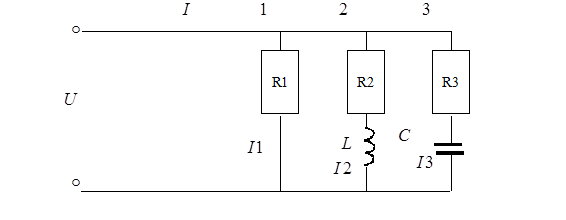Разветвленная цепь, состоящая из трех ветвей, представлена на рисунке выше. Цепь находится под общим напряжением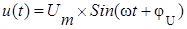 
. 
, 
, 
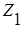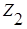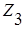- полные сопротивления ветвей 1, 2 и 3.
= 
, 
, 
.
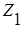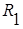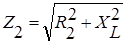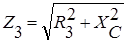Действующие значения токов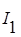 
, 
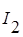и 
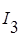в ветвях
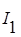= U/Z1, 
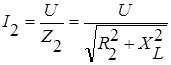и 
.
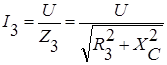При анализе параллельных ветвей для упрощения удобно использовать активные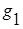 
, 
и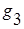 
и реактивные проводимости ветвей 
, 
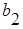и 
.
, 
, 
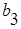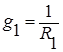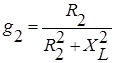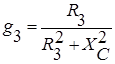, = 0, =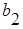 
= 
,
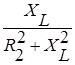
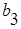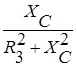полная проводимость параллельной цепи имеет вид:
y =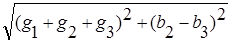 
. По закону Ома для проводимостей I = U´y.
Если 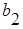- 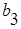=0, то имеем резонанс токов в параллельных ветвях № 2 и 3.
Общий ток I найдем по векторной диаграмме (при допущении, что ток в
1-й ветви i1(t) имеет нулевую начальную фазу).
 |
На рисунке использованы обозначения: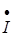 
- комплекс общего тока I,
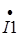- комплекс тока I1 через резистора R1,
, 
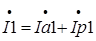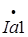- активная компонента вектора 
,
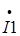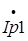- реактивная компонента вектора ,
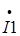- комплекс тока I2 через резистор R2 и катушку L,
, 
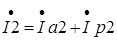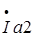- активная компонента вектора 
,
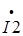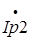- реактивная компонента вектора ,
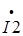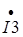- комплекс тока I3 через резистор R3 и емкость C,
, 
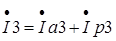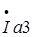- активная компонента вектора 
,
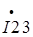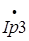- реактивная компонента вектора 
.
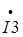Реально через ветви 1, 2 и 3 протекают токи I1, I2 и I3,
активные и реактивные составляющие комплексов токов 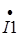, и 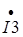используют в теории при анализе цепи.
Ia1 = Ug1, Ia2 = Ug2,
 |
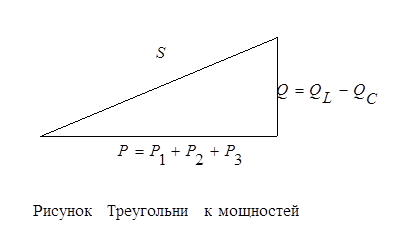Ia3 = Ug3
Ip1 = 0, Ip2 = Ub2, Ip3 = Ub3
I2 = корень квадратный
Дата добавления: 2015-08-08; просмотров: 858;