Спектры излучения.

Рассмотрим структуру щелочных металлов. Если атом щелочного металла имеет всего Z электронов, то можно считать, что 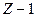электронов вместе с ядром образуют сравнительно прочный остов. В электрическом поле остова движется внешний (валентный) электрон, довольно слабо связанный с остовом атома. В некотором смысле атомы щелочных металлов являются водородоподобными, но не совсем. Дело в том, что внешний электрон несколько деформирует электронный остов и тем самым искажает поле, в котором электрон движется.

Решение уравнения Шредингера для внешнего электрона приводит к тому, что дозволенные значения энергии 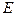в области 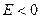(для связанных состояний внешнего электрона) будут зависеть не только от главного квантового числа (как в случае атома водорода), но и от орбитального квантового числа :

,

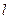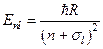где 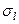– ридберговская поправка (квантовый дефект), зависящая от .

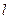Исследования спектров ионов щелочных металлов показало, что момент импульса атомного остова равен нулю. Следовательно, орбитальный момент атома щелочного металла оказывается равным моменту его внешнего электрона и определяется квантовым числом .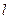

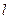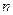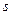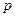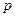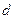Излучение и поглощение происходит в результате перехода внешнего электрона с одного уровня на другой. Однако возможны только переходы, при которых орбитальное квантовое число внешнего электрона меняется на единицу (главное квантовое число может изменяться на любое целое число). Это означает, что разрешенными являются переходы лишь между - и -состояниями, между - и -состояниями и т. д.

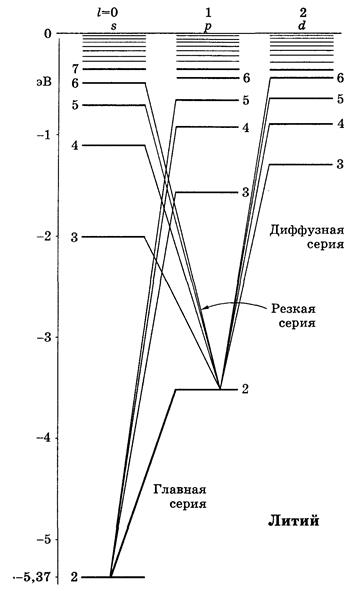
Схема спектра атома лития

Спектр атома лития имеет следующие серии (записаны в символьном виде):

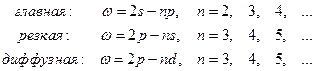
В явном виде частота 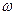испускаемой линии главной серии лития равна

,

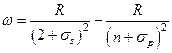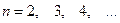
Ридберговские поправки в пределах каждой серии практически постоянные, но меняются от серии к серии.

Экспериментально обнаружено, что спектральные линии атомов щелочных металлов являются двойными (дублетами), т. е. образуют тонкую структуру.

Тонкая структура, т. е. расщепление спектральных линий, вызвана расщеплением самих энергетических уровней. Но последнее никак не следует из решения уравнения Шредингера. А дело в следующем. Электрон обладает собственным моментом – спином. Полный момент импульса электрона равен сумме орбитального момента и спинового:

,

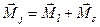где 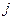– квантовое число полного импульса, 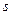– спиновое квантовое число.

Полный момент электрона квантуется

, .

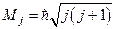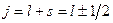Орбитальный и спиновый моменты взаимодействуют друг с другом. Энергия этого взаимодействия зависит от взаимной «ориентации» моментов, что и приводит к расщеплению энергетических уровней.