Двухпроводная линия

В технике связи часто возникает необходимость осуществлять направленную передачу электромагнитных волн от источника к потребителю, чтобы ограничить рассеяние передаваемой энергии в пространстве и/или воспрепятствовать несанкционированному доступу к передаваемой информации. Простейшей с точки зрения технической реализации направляющей системой является двухпроводная линия, в которой передача энергии осуществляется токами, протекающими по проводникам.

Двухпроводная линия представляет собой два проводника, разделенных воздушным промежутком или специальным диэлектриком. Проводники, образующие линию, имеют активные сопротивление и индуктивность. Их можно рассматривать как обкладки конденсатора, следовательно, линия обладает определенной емкостью. Кроме того, среда между проводниками обладает конечной проводимостью. Эти параметры непрерывно распределены по длине линии, и ее называют цепью с распределенными параметрами. 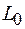Их общая величина зависит от длины линии, поэтому двухпроводную линию принято характеризовать погонными сопротивлением , индуктивностью , емкостью и проводимостью 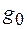. Погонные характеристики определяют соответственно сопротивление, индуктивность, емкость и проводимость единицы длины линии.

Рассмотрим особенности передачи электромагнитной энергии на примере линии без потерь ( 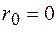, 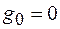). Будем считать, что начало линии (источник сигнала) находится слева, а конец линии (потребитель) – справа (рис. 78.1).

Выберем на расстоянии 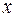от начала линии малый участок длиной 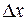. Его можно представить в виде индуктивности 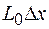и емкости 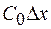. Обозначим напряжение и ток в начале участка соответственно и 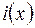, а в конце участка – 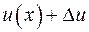и 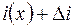. При протекании переменного тока через индуктивность 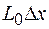в ней по закону электромагнитной индукции возникнет ЭДС индукции и тогда по второму закону Кирхгофа для выбранного участка можно записать

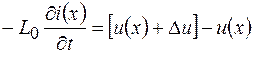. (78.1)

Силу тока, протекающего через емкость 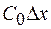, найдем по формуле 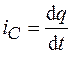. Подставляя 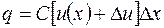и отбрасывая бесконечно малые второго порядка, получим 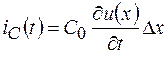. По первому закону Кирхгофа для узла А можно записать

. (78.2)

Разделив уравнения (78.1), (78.2) на 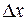, приведем их к виду

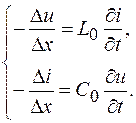
Переходя к пределу при 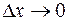, получим телеграфные уравнения, описывающие изменение напряжения и тока в двухпроводной линии:

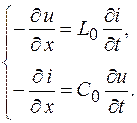(78.3)

Если источник выдает в линию переменное напряжение с частотой 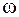, то напряжение и ток во всей линии также будут изменяться с частотой 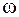, и поэтому решение телеграфных уравнений будем искать в виде 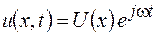и 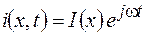, где мнимая единица обозначена как (чтобы не путать с током ), а и 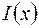– соответственно комплексные амплитуды напряжения и силы тока в точке с координатой 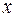. Подставляя эти решения в телеграфные уравнения, после дифференцирования и элементарных преобразований получим дифференциальные уравнения для комплексных амплитуд напряжения и силы тока:

, (78.4)

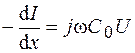. (78.5)

В этих уравнениях частные производные заменены полными, так как амплитуды напряжения и силы тока зависят только от координаты 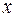. Продифференцировав обе части уравнения (78.4) по 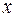и подставив вместо правую часть уравнения (78.5), получим

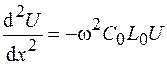. (78.6)

Уравнение (78.6) подобно дифференциальному уравнению гармонических колебаний, поэтому его решение имеет вид

, (78.7)

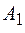где и 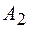– произвольные постоянные, определяемые начальными условиями, а .

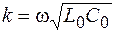Умножая комплексную амплитуду напряжения на временной множитель 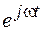, для мгновенного значения напряжения получим следующее выражение:

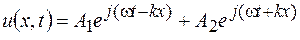. (78.8)

Из (78.8) следует, что напряжение в линии распространяется в виде двух волн. Первое слагаемое соответствует прямой волне, распространяющейся в положительном направлении оси 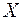, т. е. от источника к потребителю. Второе слагаемое в (78.8) соответствует волне, отраженной от конца линии. Из телеграфных уравнений (78.3) легко показать, что силу тока 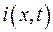также можно представить в виде прямой и отраженной волн. При этом отношение напряжения к силе тока в прямой и отраженной волнах оказывается одинаковым и равным волновому сопротивлению 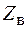двухпроводной линии:

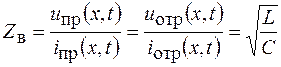. (78.9)

В линии без потерь волновое сопротивление является чисто активным, зависит от параметров линии и не зависит от частоты.

Прямая волна, дойдя до нагрузки, частично отражается от нее. Встречная волна точно также испытывает отражение от источника. Можно показать, что коэффициенты отражения волн от источника и нагрузки 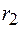равны

, (78.10)

, (78.11)

где 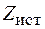и – полные сопротивления источника и нагрузки.

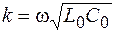Фазовая скорость распространения волны в длинной линии без потерь равна , где волновое число . Погонные индуктивность и емкость определяются конструктивными параметрами линии. Для коаксиального кабеля погонную емкость можно определить по формуле емкости цилиндрического конденсатора, полагая в ней длину конденсатора, равную 1 м, т. е.

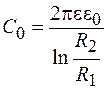, (78.12)

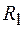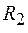где и – соответственно радиусы внешнего и внутреннего проводников; 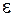– диэлектрическая проницаемость изоляции. Погонная индуктивность для коаксиального кабеля определяется выражением

. (78.13)

Тогда для фазовой скорости получим , т. е. волны напряжения и тока распространяются в линии со скоростью света.

При наличии потерь длинная линия обладает дисперсией, т. е. фазовая скорость для различных частот оказывается различной. Наличие дисперсии приводит к искажениям передаваемых по линии сигналов (расплывание импульсов), причем с ростом частоты искажения увеличиваются. По этой причине полоса частот передаваемых по линии сигналов ограничена, что необходимо учитывать при передаче информации по двухпроводной линии.

Волновой характер распространения электрического сигнала в двухпроводной линии необходимо учитывать, если ее длина соизмерима с длиной волны 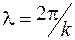. На низких частотах электромагнитное поле является квазистационарным и волновыми эффектами можно пренебречь. Однако для частот более 1 МГц длина волны в воздухе меньше 300 м и двухпроводную линию длиной несколько десятков метров уже необходимо рассматривать как цепь с распределенными параметрами.