Движение заряженных частиц в магнитном поле
Рассмотрим движение заряженной частицы в однородном магнитном поле при разных направлениях вектора скорости 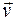 частицы относительно вектора магнитной индукции
частицы относительно вектора магнитной индукции  .
.
 1. Пусть
1. Пусть 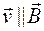 (рис. 78.1), тогда угол между
(рис. 78.1), тогда угол между 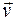 и
и  равен нулю и в соответствии с формулой (65.3) на заряд со стороны магнитного поля сила не действует. Поэтому частица будет двигаться прямолинейно с постоянной скоростью
равен нулю и в соответствии с формулой (65.3) на заряд со стороны магнитного поля сила не действует. Поэтому частица будет двигаться прямолинейно с постоянной скоростью 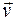 .
.
2. Пусть 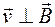 (рис. 78.2). Так как в этом случае
(рис. 78.2). Так как в этом случае 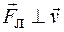 , то это означает, что сила Лоренца сообщает частице центростремительное ускорение, числовое значение скорости при этом не меняется:
, то это означает, что сила Лоренца сообщает частице центростремительное ускорение, числовое значение скорости при этом не меняется:
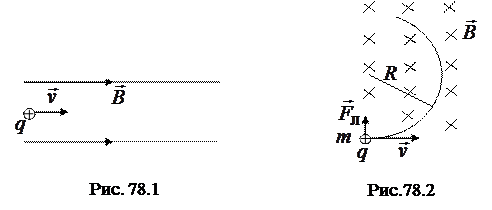 |
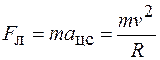 . (78.1)
. (78.1)
Из формул (65.4) и (78.1) получаем 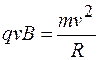 , откуда находим:
, откуда находим:
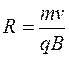 . (78.2)
. (78.2)
Из выражения (78.2) следует, что R~ 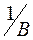 , т. е. чем сильнее магнитное поле, тем меньше радиус окружности, по которой движется частица.
, т. е. чем сильнее магнитное поле, тем меньше радиус окружности, по которой движется частица.
Найдем период обращения частицы по окружности (время одного оборота). По определению 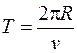 . Тогда, используя формулу (78.2), получаем:
. Тогда, используя формулу (78.2), получаем:
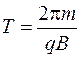 . (78.3)
. (78.3)
Отсюда видно, что период обращения частицы в магнитном поле не зависит от ее скорости. С помощью формулы (78.3) можно получить выражение для частоты 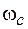 обращения заряженных частиц в постоянном магнитном поле
обращения заряженных частиц в постоянном магнитном поле  в плоскости, перпендикулярной
в плоскости, перпендикулярной  . Она называется циклотронной и равна
. Она называется циклотронной и равна
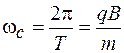 . (78.4)
. (78.4)
Циклотронная частота играет важную роль в вопросах генерации и распространения ЭМВ в плазме, находящейся в постоянном магнитном поле, в частности при распространении радиоволн в земной ионосфере.
Независимость периода обращения от скорости используют в циклотронах – циклических резонансных ускорителях тяжелых заряженных частиц – протонов и ионов. Принципиальная схема циклотрона представлена на рисунке 78.3 (вид сверху). Он представляет собой вакуумную камеру в виде двух полых полуцилиндров (дуантов), на которые подается переменное электрическое напряжение. Камера помещается в сильное однородное магнитное поле, направленное перпендикулярно плоскости дуантов.
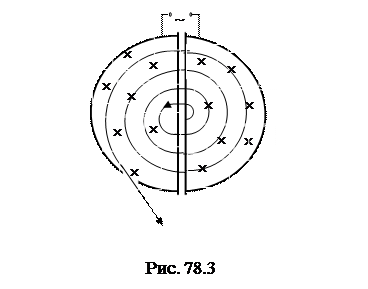 Заряд, ускоренный в промежутке между дуантами, движется внутри дуанта в магнитном поле, описывая полуокружность. Если частота изменения напряжения U совпадает с частотой обращения заряда, то при следующем попадании заряда в промежуток между дуантами вновь произойдет его ускорение. Теперь заряд будет двигаться в дуанте по окружности большего радиуса, но с тем же периодом обращения. Поэтому ча-стица будет внутри двигаться по раскручивающейся спирали, периодически увеличивая свою энергию. Так, можно ускорить протоны до энергии около 20 МэВ. При более высоких энергиях синхронизм между движением частицы и изменением ускоряющего поля нарушается вследствие релятивистских эффектов. Для сохранения синхронизма и дальнейшего ускорения частиц идут двумя путями: 1) меняют ча-стоту напряжения, поданного на дуанты, подстраивая его под частоту обращения частиц; 2) меняют индукцию магнитного поля. В первом случае ускоритель называют фазотроном, во втором – синхротроном. В ускорителе, названном синхрофазотроном (рис. 78.4), изменяются и частота ускоряющего напряжения, и магнитное поле. Уско-ряемые частицы движутся в синхрофазотроне по круговой траектории постоянного радиуса. Дуанты в нем отсутствуют. Ускорение частиц происходит на отдельных участках траектории с помощью электрического поля, создаваемого генератором напряжения меняющейся частоты. По мере увеличения скорости частицы должна расти индукция магнитного поля. Для того чтобы ускоряющее напряжение было синхронно с движением частицы, частота этого напряжения должна меняться по соответствующему закону. С помощью синхрофазотрона можно ускорить протоны до энергии порядка 500 ГэВ.
Заряд, ускоренный в промежутке между дуантами, движется внутри дуанта в магнитном поле, описывая полуокружность. Если частота изменения напряжения U совпадает с частотой обращения заряда, то при следующем попадании заряда в промежуток между дуантами вновь произойдет его ускорение. Теперь заряд будет двигаться в дуанте по окружности большего радиуса, но с тем же периодом обращения. Поэтому ча-стица будет внутри двигаться по раскручивающейся спирали, периодически увеличивая свою энергию. Так, можно ускорить протоны до энергии около 20 МэВ. При более высоких энергиях синхронизм между движением частицы и изменением ускоряющего поля нарушается вследствие релятивистских эффектов. Для сохранения синхронизма и дальнейшего ускорения частиц идут двумя путями: 1) меняют ча-стоту напряжения, поданного на дуанты, подстраивая его под частоту обращения частиц; 2) меняют индукцию магнитного поля. В первом случае ускоритель называют фазотроном, во втором – синхротроном. В ускорителе, названном синхрофазотроном (рис. 78.4), изменяются и частота ускоряющего напряжения, и магнитное поле. Уско-ряемые частицы движутся в синхрофазотроне по круговой траектории постоянного радиуса. Дуанты в нем отсутствуют. Ускорение частиц происходит на отдельных участках траектории с помощью электрического поля, создаваемого генератором напряжения меняющейся частоты. По мере увеличения скорости частицы должна расти индукция магнитного поля. Для того чтобы ускоряющее напряжение было синхронно с движением частицы, частота этого напряжения должна меняться по соответствующему закону. С помощью синхрофазотрона можно ускорить протоны до энергии порядка 500 ГэВ.
3. Пусть вектор скорости 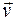 частицы образует с направлением вектора магнитной индукции
частицы образует с направлением вектора магнитной индукции  острый угол a (рис. 78.5). Разложим вектор
острый угол a (рис. 78.5). Разложим вектор 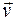 на две составляющие:
на две составляющие: 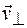 – перпендикулярную вектору
– перпендикулярную вектору  ,
, 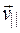 – параллельную вектору
– параллельную вектору  . Под действием силы Лоренца частицы со скоростью
. Под действием силы Лоренца частицы со скоростью 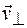 будут двигаться по окружности, радиус которой определяется формулой (78.2), т. е.
будут двигаться по окружности, радиус которой определяется формулой (78.2), т. е.
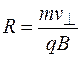 .
.
Поскольку 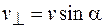 , то
, то
 |
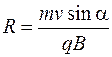 . (78.5)
. (78.5)
Так как 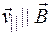 , то со скоростью
, то со скоростью 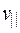 частица будет двигаться равномерно и прямолинейно. Траекторией результирующего движения частицы будет винтовая линия, осью которой является линия вектора
частица будет двигаться равномерно и прямолинейно. Траекторией результирующего движения частицы будет винтовая линия, осью которой является линия вектора  . Расстояние, на которое переместится частица за время одного оборота (за период Т), называют шагом винтовой линии h. По определению
. Расстояние, на которое переместится частица за время одного оборота (за период Т), называют шагом винтовой линии h. По определению 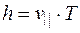 . Поскольку
. Поскольку 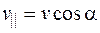 , то с учетом формулы (78.3), получаем:
, то с учетом формулы (78.3), получаем:
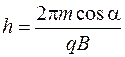 . (78.6)
. (78.6)
 Если магнитное поле неоднородное и частица движется в сторону более сильного поля, то радиус винтовой линии, как следует из формулы (78.5), будет уменьшаться. Кроме того, появляется сила, тормозящая движение (рис.78.6). Особая форма магнитного поля может заставить заряженную частицу двигаться в обратном направлении. Это используется в так называемых магнитных ловушках.
Если магнитное поле неоднородное и частица движется в сторону более сильного поля, то радиус винтовой линии, как следует из формулы (78.5), будет уменьшаться. Кроме того, появляется сила, тормозящая движение (рис.78.6). Особая форма магнитного поля может заставить заряженную частицу двигаться в обратном направлении. Это используется в так называемых магнитных ловушках.
Магнитной ловушкой называют конфигурацию магнитного поля, способную длительное время удерживать заряженные частицы внутри определенной области пространства.
В лабораторных условиях магнитные ловушки различных видов применяют для удержания плазмы с целью осуществления управляемого термоядерного синтеза.
Природной магнитной ловушкой для заряженных частиц, приходящих из космического пространства, является магнитное поле Земли (рис. 78.7). Оно неоднородно, у поверхности Земли равно в среднем 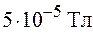 . Его происхождение связывают с конвективными движениями проводящего жидкого вещества в земном ядре. Наличие земного магнитного поля приводит к появлению зон повышенной концентрации заряженных частиц. Эти зоны называют радиационными поясами Земли. Можно выделить три таких области.
. Его происхождение связывают с конвективными движениями проводящего жидкого вещества в земном ядре. Наличие земного магнитного поля приводит к появлению зон повышенной концентрации заряженных частиц. Эти зоны называют радиационными поясами Земли. Можно выделить три таких области.
 Первый пояс, расположенный на высоте от 500 до 6 000 км от поверхности Земли, состоит в основном из протонов с энергией от 10 до 800 МэВ и электронов с энергией от десятков килоэлектронвольт до нескольких мегаэлектронвольт. В состав второго пояса, расположенного выше, входят электроны с энергией около 7 МэВ.
Первый пояс, расположенный на высоте от 500 до 6 000 км от поверхности Земли, состоит в основном из протонов с энергией от 10 до 800 МэВ и электронов с энергией от десятков килоэлектронвольт до нескольких мегаэлектронвольт. В состав второго пояса, расположенного выше, входят электроны с энергией около 7 МэВ.
 |
Область околоземного пространства, физические свойства, размеры и форма которой определяются магнитным полем Земли и его взаимодействием с потоками движущихся от Солнца заряженных частиц, называется магнитосферой (рис. 78.8). Исследования при помощи космических аппаратов показали, что магнитосфера не симметрична, а сильно вытянута в сторону, противоположную направлению на Солнце. С дневной стороны поток плазмы солнечного ветра сжимает геомагнитное поле, на ночной стороне линии магнитного поля вытягиваются в протяженный магнитный хвост.
Из других планет Солнечной системы лишь Юпитер и Сатурн обладают собственными магнитными полями, достаточными для создания магнитных ловушек. Так, поле Юпитера достигает 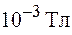 . Среднее значение общего магнитного поля Солнца составляет
. Среднее значение общего магнитного поля Солнца составляет 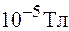 , однако в областях солнечных пятен оно достигает десятых долей тесла. По современным представлениям особенно большие (~
, однако в областях солнечных пятен оно достигает десятых долей тесла. По современным представлениям особенно большие (~ 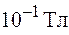 ) магнитные поля должны быть у нейтронных звезд.
) магнитные поля должны быть у нейтронных звезд.
Неоднородное магнитное поле используется для фокусировки пучка электронов магнитными линзами, которые применяются в электронных микроскопах. Электронный микроскоп – прибор для наблюдения и фотографирования многократно (до 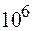 раз) увеличенного изображения объекта. В этом микроскопе в условиях глубокого вакуума (давление до
раз) увеличенного изображения объекта. В этом микроскопе в условиях глубокого вакуума (давление до 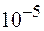 Па) вместо световых лучей используются пучки электронов, ускоренных до больших энергий (30–1000 кэВ и более). Ускоряющее напряжение достигает 100–400 кВ и выше. Электронные микроскопы обладают самой высокой разрешающей способностью, превосходя по этому параметру световые микроскопы в несколько тысяч раз (позволяют отобразить раздельно две детали объекта, находящиеся на расстоянии 0,15–0,3 нм друг от друга, т. е. позволяют наблюдать атомарную и молекулярную структуру вещества). Столь высокие разрешения достигаются благодаря чрезвычайно малой длине волны электронов.
Па) вместо световых лучей используются пучки электронов, ускоренных до больших энергий (30–1000 кэВ и более). Ускоряющее напряжение достигает 100–400 кВ и выше. Электронные микроскопы обладают самой высокой разрешающей способностью, превосходя по этому параметру световые микроскопы в несколько тысяч раз (позволяют отобразить раздельно две детали объекта, находящиеся на расстоянии 0,15–0,3 нм друг от друга, т. е. позволяют наблюдать атомарную и молекулярную структуру вещества). Столь высокие разрешения достигаются благодаря чрезвычайно малой длине волны электронов.
 |
Схематически магнитная линза изображена на рисунке 78.9. Цилиндрически симметричный электромагнит с очень острыми кольцевыми наконечниками полюсов создает в малой области очень сильное неоднородное магнитное поле. Оно фокусирует электроны, ускоренные электрическим полем и летящие вертикально через эту область. Механизм фокусировки нетрудно понять. На увеличенном изображении области вблизи наконечников полюсов (рис. 78.10) видны два электрона
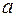 и
и 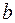 , которые покидают источник
, которые покидают источник 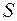 под некоторым углом по отношению к оси. Как только электрон
под некоторым углом по отношению к оси. Как только электрон 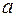 достигнет начала поля, горизонтальная компонента поля отклонит его в направлении от вас. Он приобретет боковую скорость и, пролетая через сильное вертикальное поле, получит импульс в направлении к оси. Боковое же движение убирается магнитной силой, когда электрон покидает поле, так что окончательным эффектом будет импульс, направленный к оси, плюс "вращение" относительно нее.
достигнет начала поля, горизонтальная компонента поля отклонит его в направлении от вас. Он приобретет боковую скорость и, пролетая через сильное вертикальное поле, получит импульс в направлении к оси. Боковое же движение убирается магнитной силой, когда электрон покидает поле, так что окончательным эффектом будет импульс, направленный к оси, плюс "вращение" относительно нее.
 На частицу
На частицу 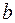 действуют те же силы, но в противоположном направлении, поэтому она тоже отклоняется по направлению к оси. На рисунке видно, как расходящиеся электроны собираются в параллельный пучок. Действие такого устройства подобно действию линзы на находящийся в ее фокусе объект. Если бы теперь вверху поставить еще одну такую же линзу, то она бы сфокусировала электроны снова в одну точку и получилось бы изображение источника
действуют те же силы, но в противоположном направлении, поэтому она тоже отклоняется по направлению к оси. На рисунке видно, как расходящиеся электроны собираются в параллельный пучок. Действие такого устройства подобно действию линзы на находящийся в ее фокусе объект. Если бы теперь вверху поставить еще одну такую же линзу, то она бы сфокусировала электроны снова в одну точку и получилось бы изображение источника 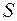 .
.
Заметим, что магнитным линзам для электронов, так же как и оптическим, присущи погрешности (аберрации), не позволяющие получить абсолютно резкое изображение. Изображение каждой точки объекта в фокальной плоскости линзы оказывается немного размытым. Существуют различные методы уменьшения аберраций.
Магнитные линзы используются также для фокусировки пучков одноименно заряженных частиц, ускоряемых в коллайдерах. Коллайдеры – это ускорители на встречных пучках, частицы которых вследствие отталкивания стремятся удалиться друг от друга в поперечном направлении. Два пучка заряженных частиц, ускоренных до заданных энергий, движутся навстречу друг другу, взаимодействуя на участке встречи. Метод встречных пучков предназначен для изучения взаимодействия сталкивающихся частиц. Важное преимущество метода в том, что в энергию взаимодействия входит полная кинетическая энергия частиц. Самые главные магнитные линзы стоят перед детектором. Их задача – сфокусировать пучок в центр детектора, где он должен будет столкнуться со встречным сгустком частиц.
Дата добавления: 2015-08-08; просмотров: 2130;
