Упражнения. 4.1. Используя Правило Счета, запишите первые 20 целых чисел в десятичной, двоичной, троичной, пятеричной и восьмеричной системах счисления

4.1. Используя Правило Счета, запишите первые 20 целых чисел в десятичной, двоичной, троичной, пятеричной и восьмеричной системах счисления.
[ Ответ ]

4.2. Какие целые числа следуют за числами:

а) 1₂;	е) 1₈;	п) F₁₆;
б) 101₂;	ж) 7₈;	м) 1F₁₆;
в) 111₂;	з) 37₈;	н) FF₁₆;
г) 1111₂;	и) 177₈;	о) 9AF9₁₆;
д) 101011₂;	к) 7777₈;	п) CDEF₁₆ ?

[ Ответ ]

4.3. Какие целые числа предшествуют числам:

а) 10₂;	е) 10₈;	л) 10₁₆;
б) 1010₂;	ж) 20₈;	м)20₁₆;
в) 1000₂;	з) 100₈;	н) 100₁₆;
г) 10000₂;	и) 110₈;	о) A10₁₆;
д) 10100₂;	к) 1000₈;	п) 1000₁₆ ?

[ Ответ ]

4.4. Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
[ Ответ ]

4.5. Какое наибольшее десятичное число можно записать тремя цифрами:

а) в двоичной системе;
б) в восьмеричной системе;
в) в шестнадцатеричной системе?

[ Ответ ]

4.6. В какой системе счисления 21 + 24 = 100?
Решение. Пусть x — искомое основание системы счисления. Тогда 100_x = 1 · x² + 0 · x¹ + 0 · x⁰, 21_x = 2 · x¹ + 1 · x⁰, 24_x = 2 · x¹ + 4 · x⁰. Таким образом, x² = 2x + 2x + 5 или x² - 4x - 5 = 0. Положительным корнем этого квадратного уравнения является x = 5.
Ответ. Числа записаны в пятеричной системе счисления.

4.7. В какой системе счисления справедливо следующее:

а) 20 + 25 = 100;
б) 22 + 44 = 110?

[ Ответ ]

4.8. Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.

[ Ответ ]

4.9. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 1011011₂;	е) 517₈;	л) 1F₁₆;
б) 10110111₂;	ж) 1010₈;	м) ABC₁₆;
в) 011100001₂;	з) 1234₈;	н) 1010₁₆;
г) 0,1000110₂;	и) 0,34₈;	о) 0,А4₁₆;
д) 110100,11₂;	к) 123,41₈;	п) 1DE,C8₁₆.

[ Ответ ]

4.10. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 125₁₀; б) 229₁₀; в) 88₁₀; г) 37,25₁₀; д) 206,125₁₀.

[ Ответ ]

4.11. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,0111₂;	г) 1011110011100,11₂;
б) 1110101011,1011101₂;	д) 10111,1111101111₂;
в) 10111001,101100111₂;	е) 1100010101,11001₂.

[ Ответ ]

4.12. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:

а) 2СE₁₆; б) 9F40₁₆; в) ABCDE₁₆; г) 1010,101₁₆; д) 1ABC,9D₁₆.
[ Ответ ]

4.13. Выпишите целые числа:

а) от 101101₂ до 110000₂ в двоичной системе;
б) от 202₃ до 1000₃ в троичной системе;
в) от 14₈ до 20₈ в восьмеричной системе;
г) от 28₁₆ до 30₁₆ в шестнадцатеричной системе.

[ Ответ ]

4.14. Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:

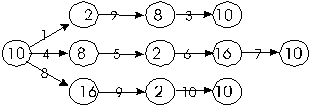
[ Ответ ]

4.15. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]

4.16. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
[ Ответ ]

4.17. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011101₂ и 1110111₂;	д) 37₈ и 75₈;	и) A₁₆ и F₁₆;
б) 1011,101₂ и 101,011₂;	е) 165₈ и 37₈;	к) 19₁₆ и C₁₆;
в) 1011₂, 11₂ и 111,1₂;	ж) 7,5₈ и 14,6₈;	л) A,B₁₆ и E,F₁₆;
г) 1011₂ , 11,1₂ и 111₂;	з) 6₈, 17₈ и 7₈;	м) E₁₆, 9₁₆ и F₁₆.

[ Ответ ]

4.18. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:

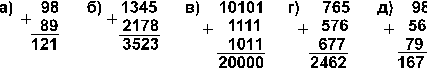
[ Ответ ]

4.19. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):

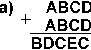
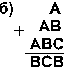
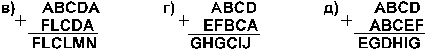
[ Ответ ]

4.20. Вычтите:

а) 111₂ из 10100₂;	д) 15₈ из 20₈;	и) 1А₁₆ из 31₁₆;
б) 10,11₂ из 100,1₂;	е) 47₈ из 102₈;	к) F9E₁₆ из 2А30₁₆;
в) 111,1₂ из 10010₂;	ж) 56,7₈ из 101₈;	л) D,1₁₆ из B,92₁₆;
г) 10001₂ из 1110,11₂;	з) 16,54₈ из 30,01₈;	м) ABC₁₆ из 5678₁₆.

[ Ответ ]

4.21. Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения:

а) 101101₂ и 101₂;	д) 37₈ и 4₈;
б) 111101₂ и 11,01₂;	е) 16₈ и 7₈;
в) 1011,11₂ и 101,1₂;	ж) 7,5₈ и 1,6₈;
г) 101₂ и 1111,001₂;	з) 6,25₈ и 7,12₈.

[ Ответ ]

4.22. Разделите 10010110₂ на 1010₂ и проверьте результат, умножая делитель на частное.
[ Ответ ]

4.23. Разделите 10011010100₂ на 1100₂ и затем выполните соответствующее десятичное и восьмеричное деление.
[ Ответ ]

4.24. Вычислите значения выражений:

а) 256₈ + 10110,1₂ ^.(60₈ + 12₁₀) - 1F₁₆;
б) 1AD₁₆ - 100101100₂ : 1010₂ + 217₈;
в) 1010₁₀ + (106₁₆ - 11011101₂) 12₈;
г) 1011₂ ^.1100₂ : 14₈ + (100000₂ - 40₈).

[ Ответ ]

4.25. Расположите следующие числа в порядке возрастания:

а) 74₈, 110010₂, 70₁₀, 38₁₆;
б) 6E₁₆, 142₈, 1101001₂, 100₁₀;
в) 777₈, 101111111₂, 2FF₁₆, 500₁₀;
г) 100₁₀, 1100000₂, 60₁₆, 141₈.

[ Ответ ]

4.26. Запишите уменьшающийся ряд чисел +3, +2, ..., -3 в однобайтовом формате:

а) в прямом коде;
б) в обратном коде;
в) в дополнительном коде.

[ Ответ ]

4.27. Запишите числа в прямом коде (формат 1 байт):

а) 31; б) -63; в) 65; г) -128.
[ Ответ ]

4.28. Запишите числа в обратном и дополнительном кодах (формат 1 байт):

а) -9; б) -15; в) -127; г) -128.
[ Ответ ]

4.29. Найдите десятичные представления чисел, записанных в дополнительном коде:

а) 1 1111000; б) 1 0011011; в) 1 1101001; г) 1 0000000.
[ Ответ ]

4.30. Найдите десятичные представления чисел, записанных в обратном коде:

а) 1 1101000; б) 1 0011111; в) 1 0101011; г) 1 0000000.
[ Ответ ]

4.31. Выполните вычитания чисел путем сложения их обратных (дополнительных) кодов в формате 1 байт. Укажите, в каких случаях имеет место переполнение разрядной сетки:

а) 9 - 2;	г) -20 - 10;	ж) -120 - 15;
б) 2 - 9;	д) 50 - 25;	з) -126 - 1;
в) -5 - 7;	е) 127 - 1;	и) -127 - 1.

[ Ответ ]

Ответы — Раздел 4. Арифметические основы компьютеров

4.1. в) троичная: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201; г) пятеричная: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34.

4.2. а) 10₂; б) 110₂; в) 1000₂; г) 10000₂; д) 101100₂; е) 2₈; ж) 10₈; з) 40₈; и) 200₈; к) 10000₈; л) 10₁₆; м) 20₁₆; н) 100₁₆; о) 9AFA₁₆; п) CDF0₁₆.

4.3. а) 1₂; б) 1001₂; в) 111₂; г) 1111₂; д) 10011₂; е) 7₈; ж) 17₈; з) 77₈; и) 107₈; к) 777₈; л) F₁₆; м) 1F₁₆; н) FF₁₆; о) A0F₁₆; п) FFF₁₆.

4.4. Четное двоичное число оканчивается цифрой 0, нечетное двоичное — цифрой 1, четное троичное — цифрами 0, 1 или 2.

4.5. а) 7; б) 511; в) 4091.

4.7. а) ни в какой; б) в шестеричной.

4.8. Основание 5.

4.9. а) 91; б) 183; в) 225; г) ³⁵/₆₄; д) 52,75; е) 335; ж) 520; з) 668; и) ⁷/₁₆; к) 83³³/₆₄; л) 31; м) 2748; н) 4112; о) ⁴¹/₆₄; п) 478²⁵/₃₂.

4.10. а) 1111101₂; 175₈; 7D₁₆; б) 11100101₂; 345₈; E5₁₆; в) 1011000₂; 130₈; 58₁₆; г) 100101,01₂; 45,2₈; 25,4₁₆; д) 11001110,001₂; 316,1₈; CE,2₁₆.

4.11. а) 11767,34₈; 13F7,7₁₆; б) 1653,564₈; 3AB,BA₁₆; в) 271,547₈; B9,B38₁₆; г) 13634,6₈; 179C,C₁₆; д) 27,7674₈; 17,FBC₁₆; е) 1425,62₈; 315,C8₁₆.

4.12. а) 1011001110₂; 1316₈; б) 1001111101000000₂; 117500₈; в) 10101011110011011110₂; 2536336₈; г) 1000000010000,000100000001₂; 10020,0401₈; д) 1101010111100,10011101₂; 15274,472₈.

4.13. а) 101101₂, 101110₂, 101111₂, 110000₂; б) 202₃, 210₃, 211₃, 212₃, 220₃, 221₃, 222₃, 1000₃; в) 14₈, 15₈, 16₈, 17₈, 20₈; г) 28₁₆, 29₁₆, 2A₁₆, 2B₁₆, 2C₁₆, 2D₁₆, 2E₁₆, 2F₁₆, 30₁₆;

4.14. а) 47₁₀ - 101111₂ - 57₈ - 47₁₀ - 57₈ - 101111₂ - 2F₁₆ - 47₁₀ - 2F₁₆ - 101111₂ - 47₁₀; б) 79₁₀ - 1001111₂ - 117₈ - 79₁₀ - 117₈ - 1001111₂ - 4F₁₆ - 79₁₀ - 4F₁₆ - 1001111₂ - 79₁₀.

4.15.

	+

+

4.16.

	x

x

4.17. а) 11010100₂; б) 10001,0₂; в) 10101,1₂; г) 11001,1₂; д) 134₈; е) 224₈; ж) 24,3₈; з) 34₈; и) 19₁₆; к) 25₁₆; л) 19,A₁₆; м) 26₁₆.

4.18. а) в 16-й; б) в 10-й; в) в 3-й; г) в 8-й; д) в 16-й.

4.19. в) А=9, B=4, C=5, D=3, F=1, L=0, M=7, N=8; г) A=3, B=6, C=2, D=5, E=9, F=7, G=1, H=0, I=4, J=8; д) A=9, B=3, C=4, D=2, E=1, F=8, G=0, H=7, I=6.

4.20. а) 1101₂; б) 1,11₂; в) 1010,1₂; г) -10,01₂; д) 3₈; е) 33₈; ж) 22,1₈; з) 11,25₈; и) 17₁₆; к) 1A92₁₆; л) -1,7E₁₆; м) 4BBC₁₆.

4.21. а) 11100001₂; б) 11000110,01₂; в) 1000000,101₂; г) 1001011,101₂; д) 174₈; е) 142₈; ж) 15.26₈; з) 55.2222₈.

4.22. 1111₂.

4.23. 1100111₂; 103₁₀; 147₈.

4.24. а) 1493₁₀; б) 542₁₀; в) 1420₁₀; г) 11₁₀.

4.25. а) 110010₂, 38₁₆, 74₈, 70₁₀; б) 142₈, 100₁₀, 1101001₂, 6E₁₆; в) 101111111₂, 500₁₀, 777₈, 2FF₁₆; г) 1100000₂, 60₁₆, 141₈, 100₁₀.

4.26. а) 00000011, 00000010, 00000001, 00000000, 10000001, 10000010, 10000011; б) 00000011, 00000010, 00000001, 00000000, 11111110, 11111101, 11111100; в) 00000011, 00000010, 00000001, 00000000, 11111111, 11111110, 11111101.

4.27. а) 00001111; б) 10111111; в) 01000001; г) невозможно.

4.28. Обратный: а) 11110110, б) 11110000, в) 10000000, г) невозможнo. Дополнительный: а) 11110111; б) 11110001; в) 10000001; г) 10000000.

4.29. а) -8; б) -101; в) -23; г) -128.

4.30. а) -23; б) -96; в) -84; г) -127.

4.31. Обратный: а) 00000111; б) 11111000; в) 11110011; г) 11100001; д) 00011001; е) 01111110; ж) переполнение; з) 10000000; и) невозможно. Дополнительный: а) 00000111; б) 11111001; в) 11110100; г) 11100010; д) 00011001; е) 01111110; ж) переполнение; з) 10000001; и) 10000000.

<8 9 101112 13 14 >

Дата добавления: 2015-08-08; просмотров: 1649;