Кинематика поступательного движения

Положение материальной точки А в декартовой системе координат в данный момент времени определяется тремя координатами x, y и z или радиусом-вектором – вектором, проведенным из начала системы координат в данную точку (рис. 1).

Движение материальной точки определяется в скалярном виде кинематическими уравнениями: x = x(t), у = y(t), z = z(t),

или в векторном виде уравнением: .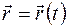

Траектория движения материальной точки – линия, описываемая этой точкой при её движении в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Материальная точка, двигаясь по произвольной траектории, за малый промежуток времени Dt переместиться из положения А в положение В, пройдя при этом путь Ds, равный длине участка траектории АВ (рис. 2).

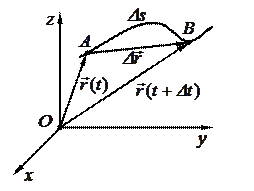
Рис. 1 Рис. 2

Вектор 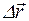, проведенный из начального положения движущейся точки в момент времени t в конечное положение точки в момент времени(t+Dt), называется перемещением,то есть .

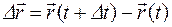Вектором средней скорости 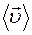называется отношение перемещения 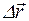к промежутку времени Dt , за который это перемещение произошло:

.

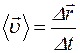Направление вектора средней скорости 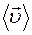совпадает с направлением вектора перемещения .

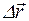Мгновенной скоростью 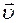(скоростью движения в момент времени t) называется предел отношения перемещения 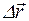к промежутку времени Dt, за который это перемещение произошло, при стремлении Dt к нулю:

,

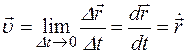где – первая производная от функции 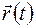по времениt, которую принято обозначать также в виде .

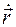Вектор мгновенной скорости 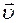направлен по касательной, проведенной в данной точке к траектории в сторону движения. При стремлении промежутка времени Dt к нулю модуль вектора перемещения 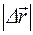стремится к величине пути Ds, поэтому модуль вектора 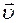может быть определен через путь Ds:

.

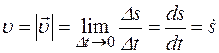Если скорость движения точки со временем изменяется, то быстрота изменения скорости движения точки характеризуется ускорением.

Средним ускорением 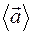в интервале времени от t до (t + Dt) называется векторная величина, равная отношению изменения скорости 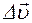( 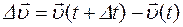) к промежутку времени Dt, за который это изменение произошло: .

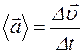Мгновенным ускорением 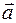или ускорением движения точки в момент времени t называется предел отношения изменения скорости 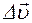к промежутку времени Dt, за который это изменение произошло, при стремлении Dt к нулю:

,

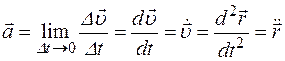где 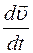– первая производная от функции 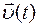по времениt,

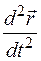– вторая производная от функции 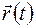по времениt.

Эти производные принято обозначать соответственно в виде: 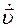и .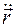

Вектор ускорения 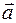может быть разложен на две составляющие:тангенциальную 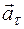и нормальную 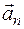, то есть:

.

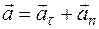Тангенциальная составляющая 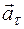определяет быстроту изменения модуля скорости : .

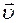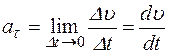Вектор 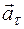направлен по касательной к траектории движения и для ускоренного движения совпадает с направлением вектора скорости 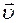, а для замедленного движения – противоположен вектору скорости .

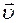Нормальная составляющая 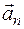определяет быстроту изменения направления скорости : ,

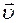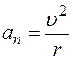где r – радиус кривизны траектории движения.

Вектор 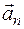направлен по нормали к траектории движения к центру ее кривизны (поэтому нормальную составляющую ускорения называют также центростремительным ускорением).