Схема 33. Основополагающие концепции и методологические принципы квантовой механики.
| v Концепция корпускулярно-волнового дуализма: «Каждый элемент материи имеет свойства волны и частицы». |
| v Концепция дискретности материи: «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| v Концепция вероятностного подхода: «Квантовая механика отказывается от стремления к точным предсказаниям того, что произойдёт при опредеоённых условиях. Мало того, это считается невозможным – единственное, что можно предсказать - это вероятность тех или иных событий. Так, что в квантовой механике мы должны удовлетвориться расчётом вероятностей, при этом считать, что такова природа на самом деле». |
v Принцип неопределённости:
Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга:
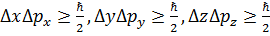 и и 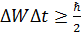 . и находит отражение в принципе дополнительности Н. Бора. . и находит отражение в принципе дополнительности Н. Бора.
|
| v Принцип дополнительности: «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| v Принцип соответствия: «Любая новая более общая теория, являющаяся развитием предыдущих классических теорий, справедливость которых была экспериментально установлена для определенных групп явлений, не отвергает эти классические теории, а включает их в себя. В определенных случаях существует возможность предельного перехода новой теории в старую». |
| v Принцип простоты. «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) 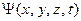 , которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
, которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
 ,
,
а в случае стационарных состояний вид его упрощается
 ,
,
где  - оператор Гамильтона.
- оператор Гамильтона.
Квадрат модуля волновой функции 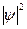 равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема,
равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема,  .
.
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 34), квантовые статистики (см. схему 35) и квантовые числа микрочастиц (см. схему 36).
Дата добавления: 2015-08-08; просмотров: 671;
