Бордың кванттық теориясы

Резерфорд ұсынған модельге сәйкес атомның +Ze заряды бар өте кішкене,бірақ ауыр ядросы, оның төңірегінде z электрон болады. Бірақ атомның ядролық (планетарлық моделі) классикалық физика заңдары тұрғысынан орнықсыз. Өйткені классикалық электродинамика заңдарына сәйкес:

1. Үдемелі қозғалатын зарядталған бөлшек (электрон) электромагниттік энергияны (жарық) үздіксіз шығаруға тиіс.

2. Осы жарықтың жиілігі электронның ядроны айналу жиілігіне тең болуы керек.

Демек, осы модельге сәйкес атомның толық энергиясы үздіксіз кеми беруге, ал айналу жиілігі үздіксіз арта беруге тиіс.осы жағдайда өте аз уақыт ішінде (10^-8с) электрон ядроға құлап,атом өз өмірін сүруін тоқтататындығын есептеп,көз жеткізугеболады.осы тұйыққа тірелуден шығу жолын 1913 ж. дания физигі Нильс Бор тапты. Бор өзінің жорамалдарын 2 постулат түрінде ұсынды.

1. Классикалық механика тұрғысынан атомда мүмкін болатын шексіз болатын көп электрон орбиталары ішінен, 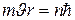белгілі кванттық шарттарды қанағаттандыратын тек кейбір дискретті орбиталар іске асады. Электрон осы станционарлық орбиталар бойымен үдей қозғалғанмен ешбір электромагниттік толқын жарық шығармайды. Осындай орбиталарға сай атомның станционарлық күйдегі энергиясының дискретті мәндері (Е₁ ,Е₂ ,Е₃ ) болады.

2. Электрон бір станционарлық күйден екінші станционарлық күйге көшкенде ғана жарық энергиясы 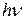кванттары түрінде шығарылады немесе жұтылады.

Жарық квантының шамасы араларында электрон кванттық көшу жалайтын станционарлық күйлер энергиясының айырмасына тең.

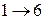жұтылу ,

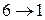шығарылады

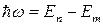
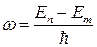жиілігі фотон шығарылады.

Осы теңдік Бордың жиіліктер ережесі деп аталады.

Бор 1913 жылы сутегі атомының классикалық емес бірінші сандық теориясын жасады.Электрон массасы сутегі ядросының массасынан 1836 есе кіші болғандықтан, электронмен салыстырғанда ядро шексіз ауыр, демек ол қозғалмай тыныштықта тұрады деп санауға болады.

Алдымен сутегі атомы үшін станционарлық орбиталар радиусын, электронның орбитадағы жылдамдығын және айналу жиілігін табайық . Егер ядроның заряды Z_e (сутегі үшін z=1) электрон заряды е, олардың ара қашықтығы r болса, онда олардың өзара кулондық тартылыс күші орталыққа (центрге) тартқыш болады. Электронның қозғалыс теңдеуі келесі түрде беріледі.

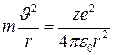
Бордың бірінші постулаты бойынша электрон тек станционар бойымен қозғала алады,ондай орбиталар бойымен қозғалған е-ның импульсі моменті 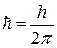шамасына еселі болады, яғни 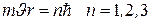. Сонымен электронның импульс моменті квантталған және оның ұлықсат етілген мәндері 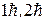болады.

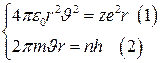
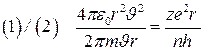
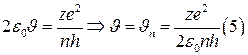
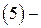ші өрнекті 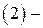ге апарып қоямыз.

Электронның орбитадан толық энергиясы кинетикалық энергия мен потенциалдық энергиясының қосындысына тең.

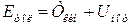
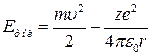
e-теріс болғанддықтан минус таңбасы қойылады.

табылған жылдамдық пен радиус өрнектерін ескерсек онда энергия

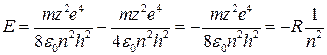
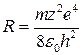Ридберг тұрақтысы

Электронның орбита бойынша 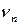айналу жиілігі мен оның сызықтық 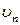жылдамдығы мына өрнек арқылы байланысқан:

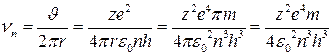
есте ұстайтын нәрсе,бұл шама, атом шығаратын сәуле жиілігі емес.

Импульс моменті (1) шартты қанағаттандыратын кванттық жүйелердің бірінде тұрған атом энергия шығармайды. Осы күйлер немесе сәуле шығармайтын орбиталар, станционарлы күйлер деп аталады. n=1 мәніне сәйкес келетін, энергиясы ең аз күй, негізгі немесе қалыпты күй деп аталады, өйткені осы күйлерде атом уақыттың көп бөлігін өткізеді. n=2,3,4…мәндерге сәйкес келетін күйлер қозған күйлер деп аталады, өйткені осы күйлердің кез-келгенінде атом негізгі күйге қарағанда көбірек энергия қабылдайды.

Z=1 N=1 сутегі атомындағы электронның ең кіші орбитасының радиусын табу үшін формулаға қоямыз

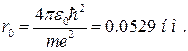
Бұл Бор радиусы деп аталады.