Жарық дисперсиясы. Дисперсияның электрондық теориясы
Жарық дисперсиясы
 Жарық дисперсиясы деп n сыну көрсеткішінің
Жарық дисперсиясы деп n сыну көрсеткішінің 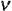 жарық жиілігіне (λ толқын ұзындығына) тәуелділігін айтады (немесе жарық толқынның
жарық жиілігіне (λ толқын ұзындығына) тәуелділігін айтады (немесе жарық толқынның 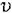 фазалық жылдамдығының осы толқын
фазалық жылдамдығының осы толқын 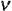 жиілігіне тәуелділігі).
жиілігіне тәуелділігі).
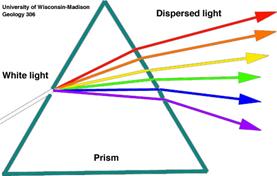
Ақ жарық шоғының призмадан өткен кездегі спектрге жіктелуі дисперсияның салдары болып табылады. Дисперсия тек монохромат емес толқын таралғанда пайда болады.
Призмадағы жарық дисперсиясын қарастырайық. Айталық, монохромат сәуле α1
бұрышымен сыну көрсеткіші n және сыну бұрышы Апризмаға түссін.
Призманың сол және оң қабырғаларынан екі рет сынғыннан кейін сәуле φ бұрышына ауытқиды:
 φ=(α1-γ1)+(α2-γ2)= α1+α2-A
φ=(α1-γ1)+(α2-γ2)= α1+α2-A
Егер А және α1 бұрыштары аз болса (яғни, α2 , γ1жәнеγ2аз болады), онда
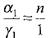 және
және 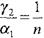 . γ1 +γ2 = Aболғандықтан,
. γ1 +γ2 = Aболғандықтан,
α2 =nγ2=n(A- γ1)=n(A- α1/n)=nA-α1, бұдан α1+α2= nA.
Сол себептіφ =A(n-1) – сәулелердің призмадан ауытқу бұрышы неғұрлым үлкен болса, соғұрлым призманың сыну бұрышы үлкен болады.
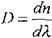 - шамасы заттың дисперсиясы деп аталады. Барлық мөлдір заттар үшін сыну көрсеткіші толқын ұзындығы өскенде кемиді:
- шамасы заттың дисперсиясы деп аталады. Барлық мөлдір заттар үшін сыну көрсеткіші толқын ұзындығы өскенде кемиді:
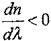 (суретке қараңыз). Мұндай дисперсия қалыпты (немесе теріс) деп аталады. Қатты жұтылу сызықтар мен жолақтар маңындағы қисықтың жолы n(λ) – дисперсия қисығы– кері:
(суретке қараңыз). Мұндай дисперсия қалыпты (немесе теріс) деп аталады. Қатты жұтылу сызықтар мен жолақтар маңындағы қисықтың жолы n(λ) – дисперсия қисығы– кері:
 ЖҮТ есептерін қорғауМұндай дисперсия аномальды дисперсия деп аталады. Призмалық спектографтардың жұмыс істеу принципі қалыпты дисперсия құбылысына негізделген. Сәулелердің призмадан ауытқу бұрышы сыну көрсеткішіне тәуелді, ал ол өз кезегінде толқын ұзындығына тәуелді. Сол себепті призма ақ жарықты спектрге жіктейді, бұл жағдайда қызыл сәулелер (толқын ұзындығы ұзын) азырақ, ал күлгін сәулелер (толқын ұзындығы қысқа) көбірек бұрышқа аутқиды.
ЖҮТ есептерін қорғауМұндай дисперсия аномальды дисперсия деп аталады. Призмалық спектографтардың жұмыс істеу принципі қалыпты дисперсия құбылысына негізделген. Сәулелердің призмадан ауытқу бұрышы сыну көрсеткішіне тәуелді, ал ол өз кезегінде толқын ұзындығына тәуелді. Сол себепті призма ақ жарықты спектрге жіктейді, бұл жағдайда қызыл сәулелер (толқын ұзындығы ұзын) азырақ, ал күлгін сәулелер (толқын ұзындығы қысқа) көбірек бұрышқа аутқиды.
Дисперсияның электрондық теориясы
Лоренцтің дисперсияның электрондық теориясы жарық дисперсиясын толқынның айнымалы электромагниттік өрісінде мәжбүр тербеліс жасайтын және заттың құрамына кіретін зарядталған бөлшектердің электромагниттік толқынмен әсерлесуінің нәтижесі ретінде қарастырады.
Ортаның абсолютті сыну көрсеткіші 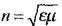 , мұндағы
, мұндағы 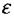 - ортаның диэлектрлік өтімділігі,
- ортаның диэлектрлік өтімділігі,  - магниттік өтімділік. Спектрдің оптикалық аймағында барлық заттар үшін
- магниттік өтімділік. Спектрдің оптикалық аймағында барлық заттар үшін 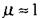 , сондықтан
, сондықтан 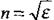 .
.
Лоренц теориясы бойынша, жарық дисперсиясы 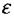 –нің жарық толқынының жиілігіне (толқын ұзындығына) тәуелділігінің нәтижесі. Анықтама бойынша
–нің жарық толқынының жиілігіне (толқын ұзындығына) тәуелділігінің нәтижесі. Анықтама бойынша
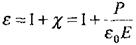
Мұндағы 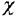 – ортаның диэлектрлік қабылдағыштығы,
– ортаның диэлектрлік қабылдағыштығы, 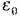 - электрлік тұрақты, Р және Е поляризацияланғыштық пен сыртқы электр өрісі кернеулігінің лездік мәндері.
- электрлік тұрақты, Р және Е поляризацияланғыштық пен сыртқы электр өрісі кернеулігінің лездік мәндері.
Спектрдің оптикалық аймағында жарық толқынының электр өрісінің тербеліс жиілігі жоғары ( 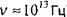 ), сол себепті диэлектриктердің ориентациялық поляризациясы мардымсыз, және электрондық (деформациялық) поляризация негізгі роль атқарады – жарық толқын өрісінің электрлік құраушысының әсерінен электронның жасайтын мәжбүр тербелістері.
), сол себепті диэлектриктердің ориентациялық поляризациясы мардымсыз, және электрондық (деформациялық) поляризация негізгі роль атқарады – жарық толқын өрісінің электрлік құраушысының әсерінен электронның жасайтын мәжбүр тербелістері.
Айталық, тек бір, атом ядросымен элсіз байланыс жасайтын, сыртқы электрон ғана мәжбүр тербеліс жасасын – оптикалық электрон. Онда атомның дипольдік моменты р=ех, мұндағы е – электрон заряды, х– жарық толқынның электр өрісінің әсерінен электронның ығысуы.
Поляризацияланғыштықтың лездік мәні Р=n0p=n0ех, мұндағы n0- диэлектриктегі атомдардың концентрациясы. Бұдан:
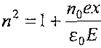
Айталық, сыртқы өріс Е гармониялық заңдылық бойынша өзгерсін 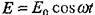 . Сонда электронның мәжбүр тербелісінің теңдеуі (түскен толқын әнергиясы жұтылуының нәтижесінде пайда болған кедергі күші ескерілмеген кезде):
. Сонда электронның мәжбүр тербелісінің теңдеуі (түскен толқын әнергиясы жұтылуының нәтижесінде пайда болған кедергі күші ескерілмеген кезде):
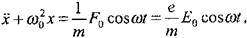
Мұндағы 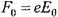 - жарық толқынының өрісі тарабынан электронға әсер ететін күштің амплитудалық мәні,
- жарық толқынының өрісі тарабынан электронға әсер ететін күштің амплитудалық мәні, 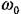 - электронның меншікті тербеліс жиілігі, m - электронның массасы.
- электронның меншікті тербеліс жиілігі, m - электронның массасы.
Бұл теңдеудің шешімі: 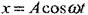 , мұндағы
, мұндағы


сондықтан:

Алынған тәуелділік дисперсия құбылысын сипаттайды: n =n(ω).
Бұл тәуелділіктің графигі суретте келтірілген. ω0айналасындағы n– нің үзілісті болуы ортаның кедергі күшін ескермегендіктің салдары (ортаның электромагниттік толқындарды жұтуы).
Егер жұтылу ескерілсе, ω0 аймақта n(ω) тәуелділігі АВ пунктир сызықтарымен көрсетілген – бұл аномаль дисперсия аймағы (ω өссе, n азаяды).
Қалған бөлік қалыпты дисперсияны сипаттайды (ω өссе, n өседі).
Жалпы жағдайда, егер затта массалары miәр түрлі eiзарятар болса, және бұл зарядтар әр түрлі ω0iменшікті жиілікте мәжбүр тербеліс жасайтын болса, онда
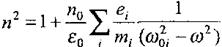
n(ω)қисығының әрбірω0iменшікті жиіліктің жанында ерекшеліктері болады.
Дата добавления: 2015-08-08; просмотров: 8429;
