Измерение количества информации

Информацию по-разному измеряют в быту, в технике и в теории информации.

Измерение информации в быту произвести очень сложно. Рассмотрим пример. Пусть Вы получили какое-то сообщение. В этом сообщении содержится какое-то количество информации. Как оценить, сколько информации Вы получили? Другими словами, как измерить информацию? Разные люди, получившие одно и то же сообщение, по-разному оценивают количество информации, содержащееся в нем. Это происходит оттого, что знания людей об этих событиях до получения сообщения были различными. Те, кто знал мало, сочтут, что они получили много информации. Те, кто знал больше, сочтут, что они не получили информации вовсе. Таким образом, количество информации в сообщении зависит от того, насколько ново это сообщение для получателя. При таком подходе непонятно, по каким критериям можно ввести единицу измерения информации. Следовательно, с точки зрения информации как новизны мы не можем оценить количество информации, содержащейся в научном открытии, новом музыкальном стиле и т.п.

В технике используют способ определения количества информации, который основан на подсчете числа символов в сообщении, т.е. связан с длиной сообщения и не учитывает содержания. Длина сообщения зависит от числа различных символов, употребляемых для записи сообщения. Например, слово «мир» в русском алфавите записывается тремя знаками, в английском – пятью (peace), а в КОИ-8 – 24 битами (111011011110100111110010). Каждый символ, как известно, кодируется 8-битным кодом. Но измерять с помощью бит неудобно, получаются громадные числа. Поэтому была введена более «крупная» единица измерения информации – байт. 1 байт = 8 бит. Можно заметить, что при измерении в байтах подсчитать количество информации легче – оно совпадает с количеством символов в нем. Действительно, слово «мир» занимает 3 байта. Фраза «миру мир!» содержит 72 бита или 9 байт информации.

В вычислительной технике битом называют наименьшую «порцию» памяти, необходимую для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд. Бит и байт - слишком мелкие единицы измерения. На практике чаще применяется более крупные производные единицы информации:

1 килобайт (кбайт) = 1024 байт = 2¹⁰ байт,

1 Мегабайт (Мбайт) = 1024 кбайт = 2²⁰ байт,

1 Гигабайт (Гбайт) = 1024 Мбайт = 2³⁰ байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Терабайт (Тбайт) = 1024 Гбайт = 2⁴⁰ байт,

1 Петабайт (Пбайт) = 1024 Тбайт = 2⁵⁰ байт.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.

По мере развития вычислительной техники было введено понятие информационной емкости сообщения, или информационного объема сообщения. Информационный объем сообщения – количество информации в сообщении, измеренное в битах, байтах или производных единицах (кбайтах, Мбайтах и т.д.).

Рассмотрим измерение информации в теории информации. В теории информации количеством информации называют числовую характеристику сигнала, не зависящую от его формы и содержания и характеризующую неопределенность, которая исчезает после получения сообщения в виде данного сигнала. В этом случае количество информации зависит от вероятности получения сообщения о том или ином событии. Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность равна 1) количество вероятности в сообщении о нем равно 0. Чем невероятнее событие, тем большую информацию о нем несет сообщение. Лишь при равновероятных ответах ответ «да» или «нет» несет 1 бит информации.

Успешные попытки измерения количества информации связаны с работами следующих ученых: Р. Фишера, Р. Хартли, Х. Найквиста, К. Шеннона и основаны на методах математической теории вероятностей. Общая идея состоит в том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле ее новизны или, иначе, уменьшения (снятия) неопределенности наших знаний об объекте.

Американский инженер Р. Хартли (1928 г.) предложил рассматривать процесс получения информации как выбор одного сообщения из конечного наперед заданного множества N равновероятных сообщений. При этом количество информации I, содержащееся в выбранном сообщении, определил как двоичный логарифм N.

Формула Хартли:

Допустим, происходит одно событие из двух равновозможных (как при играх «чет – нечет», «орел – решка», черное - белое, истина-ложь). Тогда, N = 2, по формуле Хартли количество информации, содержащееся в сообщении о произошедшем событии, составляет:

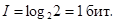
Если имеется шесть равновероятных событий (бросок игральной кости), то количество информации о наступлении одного из них:

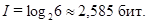
Таким образом, в формуле Хартли отражается следующий важный закон: Чем больше изначальная неопределенность наступления события, тем больше количества информации о его фактическом наступлении.

Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для определения количества информации с возможной неодинаковой вероятностью сообщений в наборе американский ученый
К. Шеннон (1948 г.) предложил следующую формулу.

Формула Шеннона:

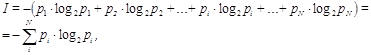
где 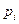- вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.

Пример.

Пусть в непрозрачном мешке находится десять шаров, из которых один черный и девять белых, тогда вероятность вытащить наугад белый шар равна 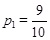, вероятность достать черный шар 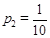. Вынимая из мешка наугад один из шаров, получаем количество информации по формуле Шеннона:

.

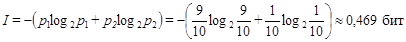Легко заметить, что если вероятности 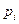всех событий равны, то для всех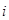

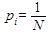
и формула Шеннона сводится к формуле Хартли.

Помимо двух рассмотренных формул определения количества информации существуют и другие, но пока они имеют меньшее распространение.