Уравнение состояния. Для определения многих физических свойств природных газов используется уравнение состояния.
Для определения многих физических свойств природных газов используется уравнение состояния.
Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используется давление, температура, объём.
Состояние газа при нормальных и стандартных условиях описывается уравнением Менделеева–Клапейрона:
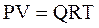, (2.17)
где Р – абсолютное давление, Па;
V – объём, м3;
Q – количество вещества, кмоль;
Т – абсолютная температура, К;
R – универсальная газовая постоянная, Па×м3/(кмоль×град).
На основе уравнения состояния газа можно рассчитать много параметров для системы нефтяного газа: плотность, мольный объём, количество молекул, число молекул, парциальные давления и др., если рассматривать уравнение состояния газа для 1 моля, т.е., Q = 1 моль. С учетом этого, уравнение состояния газа можно преобразовать следующим образом:
P·V = ∑N·R·T. (2.18)
При ∑N = 1 моль, следует, что: P·V = R·T. Зная, что масса (m) одного моля идеального газа равна его молекулярной массе (М), умножив левую и правую части на молекулярную массу и массу газа, соответственно получим:
P·V·M = m·R·T. (2.19)
Поделив обе части на V·R·T: и преобразовав 2.19, получим выражение для расчета плотности:
P·M / R·T = m / V, m / V = M·P / R·T, r = M·P / R·T. (2.20)
Рассмотрим пример. Дан один моль метана CH4.
Найти его плотность?
Решение. Зная, что молекулярная масса метана равна 16 г/моль и метан занимает объём при н.у. = 22,414 л, а при с.у. = 24,055 л, найдем:
1. rCH4 (н.у.) = 16/22,414 = 0,717 (г/л);
2. rCH4 (с.у.) = 16/24,055 = 0,665 (г/л).
Плотность смеси газовых компонентов рассчитывают с учетом средней молекулярной массы смеси газа (Mсм), как отношение его молекулярной массы к его мольному объёму (Vм). Например, при нормальных условиях (н.у.) она будет рассчитываться по выражению:
rсм = Mсм / 22,414. (2.21)
Из расчетов и из выражений 2.20, 2.21 следует, что плотность газа с возрастанием температуры будет уменьшаться, а с возрастанием давления (2.20) будет расти.
Рассмотрим другой пример. Определить плотность метана СН4 при избыточном давлении, например при давлении 3,5 атм и температуре 0°С. Решение. В этом случае общее давление в системе будет равно:
Р = (3,5 + 1) = 4 (атм).
Зная, что молекулярная масса метана = 16 г/моль, универсальная газовая постоянная (R) = 0,08206 атм•л/(К•моль), а температура (T) = 273,15 К, найдем плотность метана:
rCH4 = Р·М / R·T = (3,5 + 1)·16 /0,08206 ·273,15 = 3,21 (г/л).
Относительная плотность газов рассчитывается по отношению к плотности воздуха, определенного при тех же условиях:
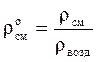. (2.22)
При нормальных условий (н.у.) плотность воздуха (ρвозд) » 1,293; при стандартных условий (с.у.) - ρвозд » 1,205.
Если плотность газа (ρо) задана при атмосферном давлении = 0,1013 МПа, то пересчёт её на другое давление (Р) при той же температуре для идеального газа производится по формуле:
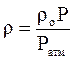. (2.23)
Рассмотрим пример. Для условий задачи, рассмотренной выше (см. пример раздела 2.2) можно рассчитать абсолютные (r) и относительные (ρосм) плотности смеси, используя правое выражение (2.16) для расчета молекулярной массы:
Мсм = 100 / (36,5 / 16 +17,2 / 30 +19,8 / 44 +14,7 / 58 +11,8 / 72)
= 26,874 (кг/кмоль);
rcv = 26,874 / 22,41 = 1,119 (кг/м3);
ρосм (н.у.) = 1,119 / 1,293 = 0,927.
Аналогично из (2.20) находится и выражение для мольного объёма:
V = R ·T / P. (2.24)
Отсюда, мольный объём при давлениях равному 1 атм или близких к атмосферному и для физических процессов, когда не происходит изменения числа молей в системе оценивается соотношением:
V = R·T, (2.25)
где R – универсальна газовая постоянная, R = 0,08206 атм·л/(К·моль);
Т – температура, К;
Рассмотрим пример. Найти вид зависимости изменения мольного объёма газа от температуры V = f(T).
Решение. Воспользуемся выражением 2.25 и получим объём, занимаемый одним молем идеального газа при условиях задачи:
Vн.у. = 0,08206•273,15 = 22,414 (л),
Vс.у. = 0,08206•293,15 = 24,055 (л).
Любой газ при нормальных условиях (н.у. Þ Т = 0оС и Р = 760 мм рт. ст.) занимает объём равный 22,414 м3, а при стандартных (с.у. Þ Т = 20 оС и Р = 760 мм рт. ст.) объём равный 24,055 м3.
С увеличением температуры мольный объём газа увеличивается. Мольный объём газов с возрастанием температуры будет расти, а с возрастанием давления (см. 2.24) уменьшаться.
У этого уравнения есть свои граничные условия. Оно справедливо для описания поведения газов при давлениях близких к атмосферному (от 1 до 10–12 атм) и при температурах до 20оС. При повышенном давлении газ сжимается и его состояние отличается от поведения идеальных газов.
Дата добавления: 2015-08-08; просмотров: 1915;