Потенциальная энергия системы материальных точек

Рассмотрим систему, состоящую из многих материальных точек. Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие на материальные точки системы, зависят только от конфигурации системы (т.е. только от координат материальных точек) и сумма работ этих сил при перемещении системы из одного положения в другое не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными. В этом случае для системы материальных точек также можно ввести понятие потенциальной энергии системы, обладающей свойством (7): 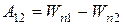, (8)

где 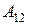- полная работа консервативных сил, действующих на материальные точки системы при переходе ее из конфигурации 1 в конфигурацию 2; 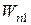и 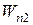- значения потенциальной энергии системы в этих конфигурациях.

Связь между силой, действующей на тело в данной точке поля, и его потенциальной энергией определяется по следующим формулам:

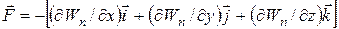(9)

или 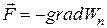, (10)

где – называется градиентом скалярной функции 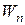; 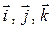– единичные векторы координатных осей;

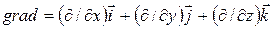. (11)

Часто формулу (9) записывают также в ви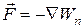де , где 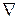– оператор набла, определяемый по формуле (11).