Затухающие колебания
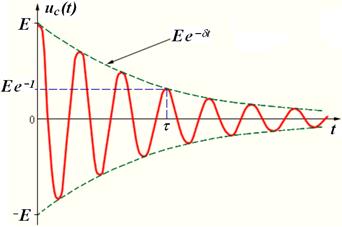
Все реальные контуры содержат электрическое сопротивление 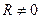 . Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в тепло, и колебания становятся затухающими (рис. 17.2).
. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в тепло, и колебания становятся затухающими (рис. 17.2).
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям пружинного маятника при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: 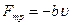 . Коэффициент
. Коэффициент 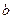 в этой формуле аналогичен сопротивлению
в этой формуле аналогичен сопротивлению 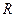 в электрическом контуре.
в электрическом контуре.
Дифференциальное уравнение свободных затухающих колебаний в контуре, который состоит из катушки индуктивности 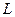 , конденсатора
, конденсатора 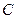 и резистора
и резистора 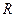 , имеет вид
, имеет вид
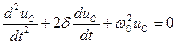 , (17.7)
, (17.7)
где 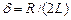 - коэффициент затухания.
- коэффициент затухания.
|
| Рис. 17.2 |
Напряжение на конденсаторе 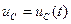 резонансного контура в случае затухающих колебаний
резонансного контура в случае затухающих колебаний
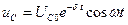 , (17.8)
, (17.8)
где 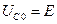 - начальное напряжение на конденсаторе. Скорость затухания зависит от электрического сопротивления
- начальное напряжение на конденсаторе. Скорость затухания зависит от электрического сопротивления 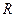 контура. Интервал времени
контура. Интервал времени
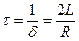 , (17.9)
, (17.9)
в течение которого амплитуда колебаний уменьшается в 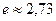 раза, называется временем затухания (рис. 17.2).
раза, называется временем затухания (рис. 17.2).
Добротность 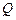 колебательного контура зависит от всех параметров контура
колебательного контура зависит от всех параметров контура 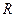 ,
, 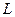 и
и 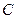 :
:
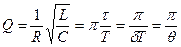 ,
, 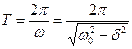 . (17.10)
. (17.10)
Здесь 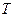 - период затухающих колебаний,
- период затухающих колебаний, 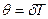 Видно, что добротность пропорциональна числу полных колебаний
Видно, что добротность пропорциональна числу полных колебаний 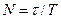 , совершаемых системой за время затухания
, совершаемых системой за время затухания 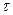 .
.
Добротность электрических контуров, применяемых в радиотехнике, составляет величину порядка нескольких десятков и даже сотен единиц.
Вычислим отношение 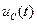 и
и 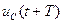
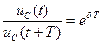 . (17.11)
. (17.11)
Оно, как и в механике, называется декрементом затухания, а его логарифм
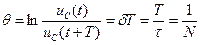 (17.12)
(17.12)
- логарифмическим декрементом затухания. Из соотношения (17.12) найдем коэффициент затухания
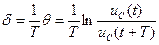 . (17.13)
. (17.13)
Частота  затухающих колебаний
затухающих колебаний
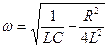 , (
, ( 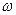 <
< 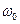 ). (17.14)
). (17.14)
Отметим, что частота 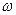 свободных затухающих колебаний в контуре с не очень высокой добротностью несколько меньше собственной резонансной частоты
свободных затухающих колебаний в контуре с не очень высокой добротностью несколько меньше собственной резонансной частоты 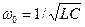 идеального контура с теми же значениями
идеального контура с теми же значениями 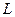 и
и 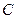 . Но при
. Но при 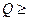 (5÷10) этим различием можно пренебречь.
(5÷10) этим различием можно пренебречь.
17.3. Вынужденные колебания в 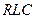 контуре
контуре
Рассмотрим последовательный резонансный контур, содержащий резистор 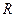 , катушку индуктивности
, катушку индуктивности 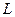 и конденсатор
и конденсатор 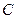 . К контуру подключен источник синусоидальной ЭДС
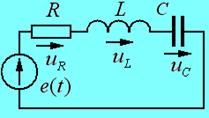
. К контуру подключен источник синусоидальной ЭДС 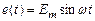 (рис. 17.3). Установившиеся колебания, возникающие в контуре под действием синусоидальной ЭДС, называютсявынужденными колебаниями.
(рис. 17.3). Установившиеся колебания, возникающие в контуре под действием синусоидальной ЭДС, называютсявынужденными колебаниями.
|
| Рис. 17.3 |
Установившиеся вынужденные колебания всегда происходят на частоте внешней ЭДС 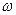 . Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник
. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник 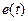 обеспечивает приток энергии к системе и, несмотря на наличие потерь
обеспечивает приток энергии к системе и, несмотря на наличие потерь 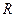 , не дает колебаниям затухнуть.
, не дает колебаниям затухнуть.
Запишем второй закон Кирхгофа для схемы на рис. 17.3:
 (17.15)
(17.15)
Учтем, что напряжения на элементах контура 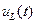 ,
, 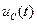 и
и 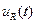 связаны с током
связаны с током 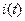 в контуре зависимостями:
в контуре зависимостями:
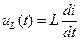 ,
, 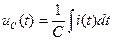 ,
, 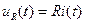 , (17.16)
, (17.16)
и преобразуем (17.15) к виду
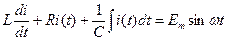 . (17.17)
. (17.17)
Поскольку
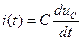 ,
, 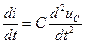 , (17.18)
, (17.18)
перепишем (17.18) в виде
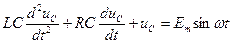 . (17.19)
. (17.19)
Введя, как и ранее, обозначения: 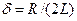 – коэффициент затухания контура,
– коэффициент затухания контура, 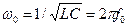 – собственная резонансная частота свободных колебаний контура,
– собственная резонансная частота свободных колебаний контура, 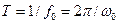 – период свободных колебаний, получим каноническое дифференциальное уравнение вынужденных синусоидальных колебаний в резонансном контуре при действии ЭДС
– период свободных колебаний, получим каноническое дифференциальное уравнение вынужденных синусоидальных колебаний в резонансном контуре при действии ЭДС 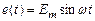 :
:
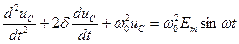 . (17.20)
. (17.20)
Дальнейший анализ проведем на комплексной плоскости ( 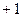 ,
, 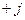 ), где
), где 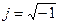 . Любое комплексное число на плоскости (
. Любое комплексное число на плоскости ( 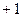 ,
, 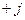 ) изображают в виде вектора. По оси абсцисс комплексной плоскости (ось
) изображают в виде вектора. По оси абсцисс комплексной плоскости (ось 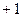 ) откладывают действительную часть комплексного числа, а по оси ординат (ось
) откладывают действительную часть комплексного числа, а по оси ординат (ось 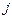 ) – мнимую часть. В качестве примера на рис. 17.4 (а) изображено число
) – мнимую часть. В качестве примера на рис. 17.4 (а) изображено число 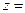
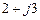 .
.
|
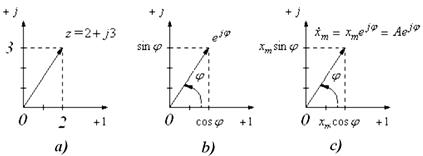
| Рис. 17.4 |
Из курса математики известна формула Эйлера:
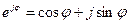 ,
, 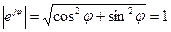 . (17.21)
. (17.21)
Комплексное число 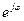 также изображают на комплексной плоскости рис. 17.4 (б) вектором, по модулю равным единице, и составляющим угол
также изображают на комплексной плоскости рис. 17.4 (б) вектором, по модулю равным единице, и составляющим угол 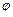 с осью вещественных чисел (осью
с осью вещественных чисел (осью 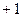 ). Положительный угол отсчитывают против часовой стрелки, отрицательный угол - по часовой стрелке.
). Положительный угол отсчитывают против часовой стрелки, отрицательный угол - по часовой стрелке.
Для анализа вынужденных колебаний,т.е. решения уравнения (17.20), воспользуемся методом комплексных амплитуд, суть которого изложена в [6]. Любую косинусоидальную или синусоидальную функцию времени 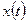 можно представить при помощи операций вычисления вещественной
можно представить при помощи операций вычисления вещественной 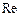 или мнимой
или мнимой 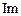 частей комплексной величины:
частей комплексной величины:
 , (17.22)
, (17.22)
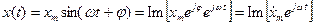 , (17.23)
, (17.23)
где 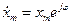 - комплексная амплитуда колебаний. Величину
- комплексная амплитуда колебаний. Величину 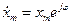 также изображают на комплексной плоскости вектором (рис. 17.4 (с)).
также изображают на комплексной плоскости вектором (рис. 17.4 (с)).
В соответствии с методом комплексных амплитуд для решения уравнения (17.20) ищем ток 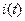 в виде:
в виде:
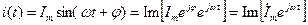 , (17.24)
, (17.24)
где 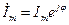 - комплексная амплитуда тока.
- комплексная амплитуда тока.
Учитывая, что
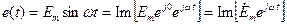 , (17.25)
, (17.25)
получим выражения для амплитуды 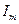 и фазы
и фазы 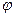 тока вынужденных синусоидальных колебаний в последовательном резонансном контуре:
тока вынужденных синусоидальных колебаний в последовательном резонансном контуре:
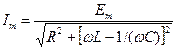 ,
, 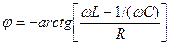 . (17.26)
. (17.26)
Полное сопротивление 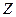 последовательного резонансного контура, его модуль
последовательного резонансного контура, его модуль 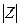 и фаза
и фаза 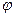
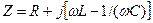 ,
, 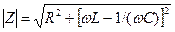 ,
,
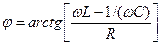 . (17.27)
. (17.27)
Отсюда сопротивление резистора 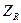 , сопротивление индуктивности
, сопротивление индуктивности  и сопротивление конденсатора
и сопротивление конденсатора 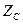 для синусоидальных колебаний:
для синусоидальных колебаний:
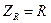 ,
, 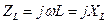 ,
, 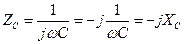 . (17.28)
. (17.28)
Комплексные амплитуды напряжений 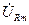 ,
, 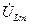 ,
, 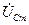 на элементах контура и комплексная амплитуда тока
на элементах контура и комплексная амплитуда тока 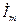 связаны законом Ома:
связаны законом Ома:
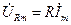 ,
, 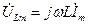 ,
, 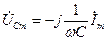 . (17.29)
. (17.29)
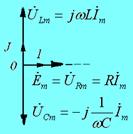
Соотношения между комплексными амплитудами напряжений и токов удобно анализировать с помощью векторных диаграмм(рис. 17.5). Из формул (17.29) следует, что вектор напряжения на резисторе 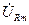 и ток в резисторе
и ток в резисторе 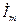 совпадают по фазе, вектор напряжения на индуктивности
совпадают по фазе, вектор напряжения на индуктивности 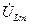 опережает ток в индуктивности
опережает ток в индуктивности 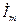 на 90º, а вектор напряжения на конденсаторе
на 90º, а вектор напряжения на конденсаторе 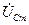 отстает от тока в конденсаторе
отстает от тока в конденсаторе 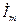 на 90º.
на 90º.
|
| Рис. 17.5 |
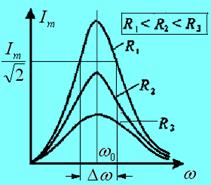
На рис. 17.6 показаны резонансные кривые колебательного контура по току (17.26), т.е. зависимость амплитуды тока 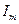 от частоты
от частоты 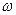 внешней синусоидальной ЭДС при разных потерях в контуре
внешней синусоидальной ЭДС при разных потерях в контуре 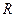 . Явление резкого возрастания амплитуды тока при равенстве частоты
. Явление резкого возрастания амплитуды тока при равенстве частоты 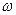 внешнего воздействия и собственной резонансной частоты свободных колебаний контура
внешнего воздействия и собственной резонансной частоты свободных колебаний контура 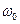 называется резонансом.Зависимости
называется резонансом.Зависимости 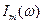 на рис. 17.6 называются также амплитудно-частотными характеристиками (АЧХ).
на рис. 17.6 называются также амплитудно-частотными характеристиками (АЧХ).
|
| Рис. 17.6 |
Видно, что чем меньше сопротивление потерь 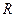 в контуре, тем выше и острее резонансная характеристика. Степень “остроты” определяется добротностью
в контуре, тем выше и острее резонансная характеристика. Степень “остроты” определяется добротностью 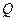 колебательной системы:
колебательной системы:
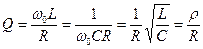 , (17.30)
, (17.30)
где 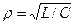 - характеристическое сопротивление контура. Добротность обычных колебательных контуров 10<
- характеристическое сопротивление контура. Добротность обычных колебательных контуров 10< 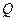 <100, при этом, чем меньше
<100, при этом, чем меньше 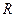 , тем больше добротность
, тем больше добротность 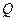 .
.
В радиотехнике колебательные контуры используются для выделения сигнала нужной радиостанции на фоне шумов или сигналов других радиостанций, при этом важным параметром является избирательность колебательной системы и чувствительность приемника. Эти параметры в значительной степени зависят от полосы пропускания 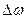 колебательной системы. Полоса пропускания
колебательной системы. Полоса пропускания 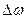 определяется по уровню
определяется по уровню 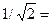 0,707 от максимума резонансной кривой
0,707 от максимума резонансной кривой 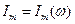 [2]:
[2]:
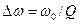 . (17.31)
. (17.31)
Видно, что чем больше добротность 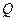 , тем меньше полоса пропускания
, тем меньше полоса пропускания 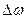 и наоборот.
и наоборот.
Из соотношений (17.29) следует, что амплитуды напряжений на резисторе  , конденсаторе
, конденсаторе 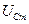 и индуктивности
и индуктивности 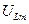 последовательного резонансного контура
последовательного резонансного контура
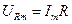 ,
, 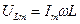 ,
, 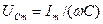 . (17.32)
. (17.32)
На резонансе 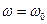 ,при этом
,при этом
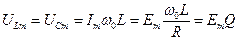 ,
, 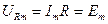 . (17.33)
. (17.33)
Видно, что на резонансе амплитуды напряжений на конденсаторе 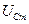 и индуктивности
и индуктивности 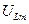 равны друг другу и в
равны друг другу и в 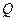 раз больше амплитуды ЭДС
раз больше амплитуды ЭДС 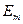 . Амплитуда
. Амплитуда 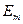 равна напряжению на резисторе
равна напряжению на резисторе  .
.
Векторная диаграмма контура на резонансе показана на рис. 17.5. Векторы напряжений на конденсаторе 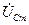 и на индуктивности
и на индуктивности 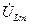 равны по величине и противоположны по направлению (фазовый сдвиг между ними равен 180º), а вектор ЭДС
равны по величине и противоположны по направлению (фазовый сдвиг между ними равен 180º), а вектор ЭДС 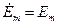 совпадает на векторной диаграмме с вектором напряжения
совпадает на векторной диаграмме с вектором напряжения 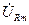 на сопротивлении
на сопротивлении 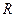 ; ток в контуре достигает максимального значения
; ток в контуре достигает максимального значения 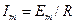 .
.
Рассчитаем теперь отношение напряжения на конденсаторе 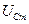 к амплитуде внешней ЭДС
к амплитуде внешней ЭДС 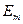 . Используя (17.32), (17.26), получим:
. Используя (17.32), (17.26), получим:
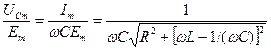 . (17.34)
. (17.34)
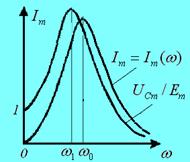
Эта зависимость показана на рис. 17.7 и называется резонансной кривой колебательного контура по напряжению (АЧХ). Она также имеет явно выраженный резонансный характер.
Отметим, что отношение напряжения на конденсаторе 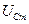 к амплитуде ЭДС
к амплитуде ЭДС 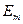 достигает максимума на частоте
достигает максимума на частоте 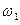 <
< 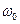 [2]:
[2]:
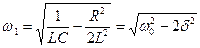 . (17.35)
. (17.35)
Обычно 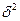 <<
<<  , при этом
, при этом 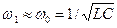 .
.
|
| Рис. 17.6 |
В инженерной практике широко используется понятие действующего значения 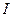 синусоидального тока
синусоидального тока 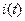 :
:
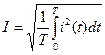 ,
, 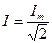 . (17.36)
. (17.36)
Дата добавления: 2015-08-04; просмотров: 1823;
