Свободные колебания. В электрических цепях, так же как и в механических системах, таких как пружинный и математический маятники

В электрических цепях, так же как и в механических системах, таких как пружинный и математический маятники, могут возникать свободные колебания. Между электромагнитными колебательными процессами и механическими колебательными явлениями много общего; эти системы дуальны (подобны) друг другу. Поэтому анализ колебательных процессов в системах различной физической природы можно проводить на основе единого подхода.

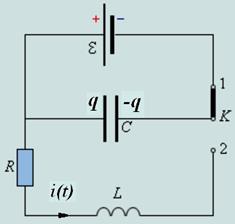
Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 17.1).

Рис. 17.1

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения источника питания 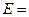õ. После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для резонансного RLC-контура, не содержащего внешнего источника ЭДС, записывается в виде

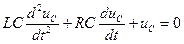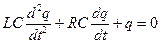, или . (17.1)

где напряжение на конденсаторе 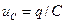, 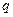- заряд конденсатора.

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии, т.е. резистивное сопротивление контура 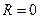. Тогда

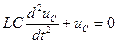, или 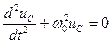, (17.2)

где

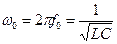(17.3)

– собственная резонансная частота свободных колебаний контура,

(17.4)

– период свободных колебаний.

Уравнение (17.2) описывает свободные колебания в LC-контуре в отсутствие потерь. Оно в точности совпадает с уравнением(6.5)свободных колебаний механического гармонического осциллятора(груза на пружине или математического маятника) в отсутствие сил трения.

Решением уравнения (17.2) является гармоническая функция времени

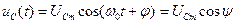, (17.5)

где 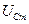- амплитуда напряжения на конденсаторе 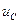, 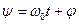- полная фаза колебаний.

В качестве примера в табл. 17.1 проведено сравнение свободных колебаний груза на пружине (пружинный маятник) и процессов в электрическом колебательном контуре, которое позволяет сделать заключение об аналогии между электрическими и механическими колебаниями.

Таблица 17.1.

Электрические величины	Механические величины
Заряд конденсатора	Координата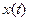
Ток в цепи	Скорость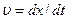
Индуктивность	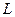Масса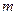
Величина, обратная электроемкости	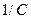Жесткость пружины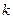
Напряжение на конденсаторе	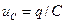Упругая сила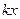
Энергия электрического поля	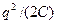Потенциальная энергия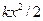
Магнитная энергия катушки	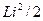Кинетическая энергия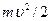
Магнитное потокосцепление	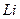Импульс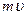

В соотношении (17.5) амплитуда 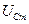и начальная фаза колебаний 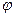определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для колебаний, который начнется в контуре (рис. 17.1) после переключения ключа K в положение 2, õ, .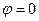

При свободных колебаниях происходит периодическое превращение электрической энергии 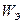, запасенной в конденсаторе, в магнитную энергию 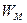катушки и наоборот. Если в колебательном контуре нет потерь энергии, то, как и при механических колебаниях в отсутствие трения, полная электромагнитная энергия системы остается неизменной:

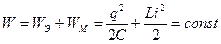. (17.6)