Многолучевая интерференция (см. лекцию №6).

Складывая когерентные волны, излучаемые равноотстоящими точечными синфазными источниками (рис. 6.1), мы получим закон распределения интенсивности в дальней волновой зоне (6.8):

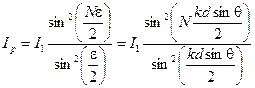(9.3)

Здесь: I_p — результирующая интенсивность в направлении θ,

I₁ — интенсивность в точке наблюдения от одного источника,

N — число источников.

Анализ уравнения (6.8) (или - что то же самое – 9.3) позволил выявить направления θ_max, в которых результирующая интенсивность принимает максимальное значение. Это так называемое условие максимумов:

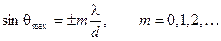(9.4)

Здесь: λ — длина волны излучения, d — расстояние между источниками.

2. Дифракционная решётка как спектральный прибор

Пусть на решётку падает нормально плоская монохроматическая волна (λ). С тем, чтобы оставаться в рамках дифракции Фраунгофера, за решёткой поместим собирающую линзу, а в её фокальной плоскости — экран наблюдения (рис. 9.3).

Рис. 9.3

Ясно, что распределение интенсивности на экране от одной щели будет определятся только направлением дифрагировавших лучей. Это означает, что дифракционные картины, создаваемые на экране любой отдельной щелью, будут совершенно одинаковы, независимо от положения щели на решётке (см. 9.1).

Теперь сложим N таких волн, дифрагировавших на щелях решётки. Результат сложения двух волн, пришедших через соседние щели, будет определятся разностью хода Δ = d sinφ. Суммарную интенсивность, возникшую от сложения N подобных волн, запишем в виде уравнения (9.3):

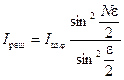. (9.5)

где: ε = k d sinφ — разность фаз волн, приходящих от двух соседних щелей.

Объединив выражение (9.1) и (9.5), получим окончательное распределение интенсивности света за дифракционной решёткой.

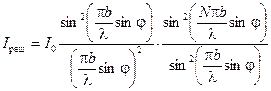. (9.6)

Здесь: I₀ — интенсивность, создаваемая одной щелью против центра линзы,

b — ширина щели,

N — число щелей,

d — период (постоянная) решётки.

Проанализируем полученный результат (9.6).

1. Интенсивность обращается в ноль, когда

b sinφ = ± k λ, (k = 1, 2, 3...) (9.7)

Это известное условие минимумов при дифракции от щели (9.2).

2. В направлениях φ, удовлетворяющих условию

d sinφ = ± mλ, (m = 0, 1, 2, 3...), (9.8)

будут наблюдаться главные интерференционные максимумы при наложении N волн. Это условие максимумов многолучевой интерференции (см. (9.4)). В этих направлениях волны от всех N щелей решетки приходят к точке наблюдения в фазе, поэтому их амплитуды складываются. Результирующая амплитуда: A_рез = N A_φ.

Интенсивность пропорциональна квадрату амплитуды, поэтому

I_реш(φ) = N ² I_щ(φ). (9.9)

Здесь: I_щ(φ) — интенсивность света, дифрагировавшего от одной щели в направлении φ.

Между двумя соседними главными максимумами располагаются (N – 1) промежуточный минимум. Эти минимумы делят расстояние между главными максимумами на N частей. Картина распределения интенсивности за дифракционной решёткой для N = 4 и 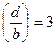, приведена на рис. 9.4. Пунктирная кривая изображает здесь интенсивность от одной щели, умноженную на N ².

Рис. 9.4.

Число главных максимумов вытекает из (9.8):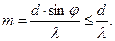

Угол между направлениями на два минимума, ограничивающих главный максимум, называется угловой шириной максимума.

Подсчитаем, например, угловую ширину нулевого максимума (см. рис. 9.4)

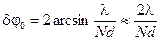(9.10)

Дифракционные решётки широко используются в качестве спектральных приборов благодаря тому, что положение главных максимумов за решёткой зависит от длины волны λ:

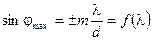(9.11)

Если на решётку падает смесь двух волн: λ и (λ + δ λ), то их нулевые максимумы, конечно, совпадут, но m-ые максимумы окажутся в разных точках экрана.

Условие m-го максимума волны λ: ,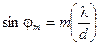

а волны (λ + δ λ): .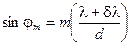

Таким образом, появляется возможность разложить с помощью дифракционной решётки смесь волн в спектр и измерить длины волн, входящих в смесь, либо их частоты.

3. Критерий Рэлея. Разрешающая сила дифракционной решётки

Одной из основных характеристик спектрального прибора (будь то дифракционная решётка или призма) является его разрешающая сила. Разрешающая сила спектрального прибора определяется безразмерной величиной

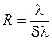(9.12)

Здесь: δλ — минимальная разность длин волн двух спектральных линий, при которой спектральный аппарат разрешает эти линии, т.е. позволяет их рассмотреть на экране наблюдения раздельно.

Выясним, от чего зависит разрешающая сила дифракционной решётки.

Согласно критерию Рэлея спектральные линии с длинами волн λ и λ’ = λ+ δλ будут разрешены, если главный максимум для одной длины волны совпадает с первым дифракционным минимумом в том же порядке для другой длины волны (рис. 9.5.б).

Рис. 9.5

Условие m-го максимума для волны λ’ = λ + δλ:

d sin φ_max = m (λ + δλ) (9.13)

Условие первого минимума, ограничивающего m-ый максимум волны λ:

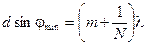(9.14)

В случае минимальной разности длин волн δλ, условия (9.13) и (9.14) описывают одну и ту же точку экрана, т.е. d sin φ_max = d sin φ_{min .}

Иными словами, условие Рэлея позволяет записать следующее равенство:

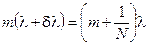или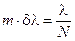

Отсюда следует, что разрешающая сила дифракционной решётки зависит только от числа её щелей (N) и от номера (m) спектра, в котором разрешаются спектральные линии.

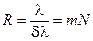(9.15)

Итог лекции 9.

1. Распределение интенсивности за дифракционной решеткой:

.

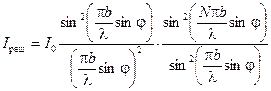Условие главных максимумов:

d sinφ = ± mλ, (m = 0, 1, 2, 3...),

.

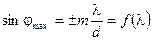Угловая ширина нулевого максимума:

.

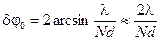2. Разрешающая сила спектрального прибора:

.

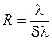Разрешающая сила дифракционной решетки: .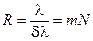

Лекция 10 «Экспериментальные основы
квантовой механики»

План лекций

1. Равновесное тепловое излучение.

1.1 Тепловое излучение абсолютно черного тела.

1.2 Классические теории Вина и Рэлея-Джинса. «Ультрафиолетовая катастрофа»

1.3 Гипотеза Планка.

2. Фотоэффект. Уравнение Эйнштейна.

2.1 Опыты Столетова.

2.2 Уравнение Эйнштейна для внешнего фотоэффекта.

К концу 19 века успехи классической механики и классической электродинамики были ошеломляющими. Казалось, что область применимости этих двух теорий безгранична.

На безоблачном горизонте физики оставалось только несколько легких облачков – нерешенных задач. Среди них – особенности теплового излучения черных тел, свойства фотоэффекта. Ждали своего объяснения и закономерности атомных спектров…

Мало кто сомневался, что эти загадки природы будут решены в ближайшее время. И уж, конечно, никто не мог предположить, что для решения этих задач придется создать принципиально новую физику – квантовую механику.