Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник».
Электрическая цепь с последовательным соединением элементов
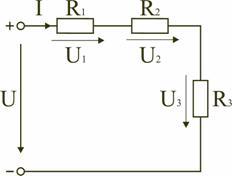
Рис. 2.1
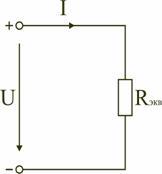
Рис. 2.2
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 2.1).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
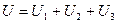 или
или 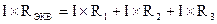 ,
,
откуда следует
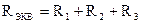 (1.6).
(1.6).
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением 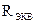 (рис. 2.2). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
(рис. 2.2). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома 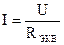 , и по вышеприведенным формулам рассчитывают падение напряжений
, и по вышеприведенным формулам рассчитывают падение напряжений 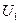 ,
, 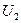 ,
, 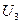 на соответствующих участках электрической цепи (рис. 2.1).
на соответствующих участках электрической цепи (рис. 2.1).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 2.3).
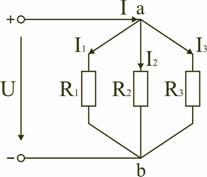
Рис. 2.3
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
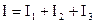 , т.е.
, т.е. 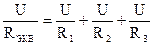 ,
,
откуда следует, что
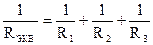 (1.7).
(1.7).
В том случае, когда параллельно включены два сопротивления 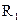 и
и 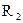 , они заменяются одним эквивалентным сопротивлением
, они заменяются одним эквивалентным сопротивлением
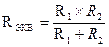 (1.8).
(1.8).
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
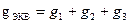 .
.
По мере роста числа параллельно включенных потребителей проводимость цепи 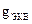 возрастает, и наоборот, общее сопротивление
возрастает, и наоборот, общее сопротивление 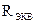 уменьшается.
уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 2.3)
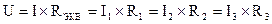 .
.
Отсюда следует, что
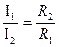 ,т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
,т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
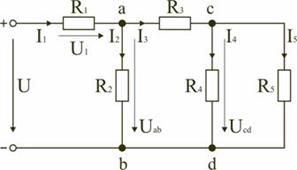
Рис. 2.4
Для цепи, представленной на рис. 2.4, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: 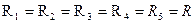 . Сопротивления
. Сопротивления 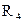 и
и 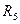 , R5 включены параллельно, тогда сопротивление участка цепи
, R5 включены параллельно, тогда сопротивление участка цепи 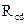 равно:
равно:
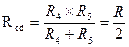 .
.
В этом случае исходную схему (рис. 2.4) можно представить в следующем виде (рис. 2.5):
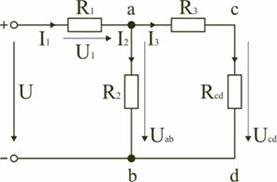
Рис. 2.5
На схеме (рис. 2.5) сопротивление 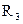 и
и 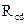 соединены последовательно, и тогда сопротивление участка цепи
соединены последовательно, и тогда сопротивление участка цепи 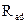 равно:
равно:
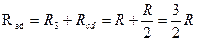 .
.
Тогда схему (рис. 2.5) можно представить в сокращенном варианте (рис. 2.6):
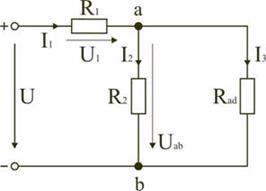
Рис. 2.6
На схеме (рис. 2.6) сопротивление 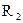 и
и 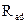 соединены параллельно, тогда сопротивление участка цепи
соединены параллельно, тогда сопротивление участка цепи 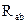 равно:
равно:
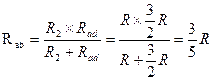 .
.
Схему (рис. 2.6) можно представить в упрощенном варианте (рис. 2.7), где сопротивления 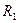 и
и 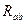 включены последовательно.
включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 2.4) будет равно:
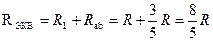
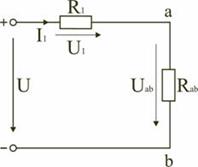
Рис. 2.7
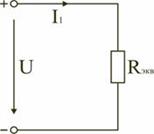
Рис. 2.8
В результате преобразований исходная схема (рис. 2.4) представлена в виде схемы (рис. 2.8) с одним сопротивлением 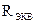 . Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 2.9). Сопротивления 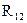 ,
, 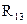 ,
, 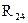 ,
, 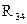 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
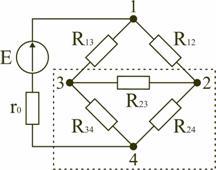
Рис. 2.9
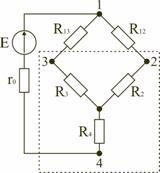
Рис. 2.10
В мостовой схеме сопротивления 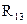 ,
, 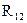 ,
, 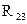 и
и 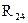 ,
, 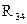 ,
, 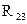 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника
соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника 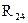
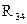
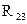 звездой
звездой 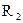
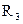
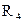 (рис. 2.10). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
(рис. 2.10). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
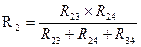 ,
, 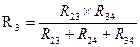 ,
, 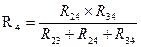 (1.9)
(1.9)
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
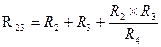 ,
, 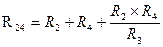 ,
, 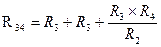 (1.10)
(1.10)
После проведенных преобразований (рис. 2.10) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 2.9)
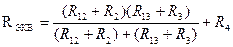 .
.
Дата добавления: 2015-08-01; просмотров: 3621;
