Непрерывные случайные величины

К непрерывным случайным величинам относятся такие случайные величину, которые могут принимать любые значения в некотором интервале числовой оси. Примером может служить результат измерения, записанный на самописце, мгновенные значения скорости теплового движения молекул газа и т.п. Так как в атом случае невозможно перечислить вое значения случайной величи-ны и указать их вероятности, непрерывную случайную величину характеризуют вероятность того, что те или иные ее значения попадают в определенные заданные интервалы области ее возможных значений. При этом вводится понятие функции плотности распределения вероятностей непрерывной случайной величины 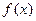- отношение вероятности 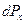попадания случайной вели - чины х в тот или иной интервал ее значений к величине этого интервала:

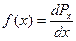(15)

Функцию f(х) называют дифференциальной функцией распределения непрерывной случайной величины X, ее размерность обратна размерности случайной величины. Тогда вероятность того, что отдельное значение случайной величины Х окажется в интервале от Х до Х + dx можно записать так:

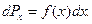(16)

График функция f(x) называется кривой функции плотности распределения вероятностей. Форма его может быть различной для распределений разных случайных величин. На рис. 1а приведена типичная кривая распределения результатов многократного измерения.

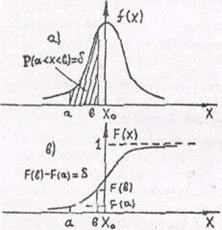Рис.1

Если функция распределения вероятностей известна, при помощи интегрирования можно найти вероятность попадания значения Х в любой интервал (-∞, х):

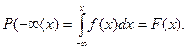(17)

Функция F(x) – первообразная для функции f(x) плотности распределения вероятностей – называется интегральной функцией рас­пределения непрерывной случайной величины. Она определяет вероятность того, что случайная величина Х примет значение меньше заданного Х (см.рис.1б). Вероятность для случайной величины Х принять значение, лежащее между а и в, равна разности интегральных функций распределения для значений в и а:

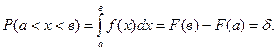(18)

На графике (рис.1а) вероятность δ численно равна заштрихованной площади, ограниченной линией графика, осью абсцисс и ординатами при Х = а и Х = в , если площадь под всей кривой принять за единицу.

Непрерывная случайная величина считается заданной, если известны ее функции распределения F(x) или f(x). При расчетах c непрерывными случайными величинами выражение f(x)dx играет ту же роль, что и вероятности Р_i для дискретных величин. Поэтому во многих формулах достаточно заменить P_i на dx, а сумму - соответствующим интегралом, чтобы перейти от формулы для дискретных величин к формуле для непрерывных величин.

Исходя из определения вероятности, очевидно, что должны иметь место следующие соотношения:

или (19)

Эти соотношения называются условиями нормировки функции плотности распределения вероятности и во многих случаях позволяют рассчитать искомую функцию f(х). Они выражают условие того, что вероятность обнаружить случайную величину во всем интервале ее возможных значений представляет достоверное событие.

Дня непрерывной случайной величина с плотностью распределения f(x) математическое ожидание М(х) и дисперсия D(x) вычисляются по формулам:

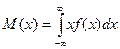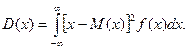или (20)

При решении практических задач имеют дело с различными законами распределения физических величин. Так, в задачах, относящихся к редким случаям (например, радиоактивный распад в проблемах флуктуации и т.п.), используется распределение Пуассона. В теории ошибок основную роль играет закон нормального распределения (распределение Гаусса).