А. Основные положения

1. Перечень предусматривает только наиболее характерные величины внутренней баллистики.

2. Частные значения переменных величин, относящихся к определенным наиболее характерным моментам, обозначаются как правило, путем добавления к обозначению переменной величины следующих подстрочных индексов:

0 - для момента начала движения снаряда;

m – для момента наибольшего давления газов;

s – для момента распада порохового зерна;

k – для момента конца горения пороха;

g – для момента вылета снаряда из канала ствола.

3. Во внутренней баллистике принимается как правило система единиц: дециметр – килограмм (сила) – секунда.

4. Наименование «пороховое зерно» понимается как отдельный элемент порохового заряда ( лента, пруток, куб, трубка, цилиндр с канальцами и.т.д.)

5. Под начальными размерами порохового зерна принимаются соответствующие размеры до начала его горения.

Предмет и задачи внутренней баллистики

Внутренняя баллистика изучает закономерности явлений и процессов, протекающих при выстреле.

Выстрел из орудия – сложный термодинамический и газодинамический, быстро протекающий высоко напряженный процесс, который характеризуется такими пора метрами: длительность выстрела – тысячные и сотые доли секунды, наибольшее давленные газов достигает 4000 – 6000 кг/ см² температура газов 2500 – 3500 К в момент их образования и 2500 – 2000 К к моменту вылета снаряда из ствола; дульная скорость снаряда достигает 1500 – 2000 м/с, а наибольшее ускорение его 50000 – 75000 g.

Начало выстрела – срабатывание капсюля – воспламенителя и зажжения воспламенителя. Воспламенитель, сгорая, создает давление газов Рв 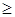50-100 кг/ см² и втечение очень малого времени (почти мгновенно) воспламеняет основной пороховой заряд. Под действием возрастающего давления газов происходит обжатие, и врезание ведущего пояска снаряда в нарезы канала ствола. Перемещение снаряда за время врезания его на полную глубину незначительно, поэтому, в некоторый промежуток времени порох горит почти в постоянном объеме. Одновременно с началом движения снаряда приходят в движение откатные части орудия. При горении заряда в канале ствола давление пороховых газов нарастает и достигает наибольшего значения - Р_m , после чего давление падает, хотя заряд продолжает гореть. В правильно спроектированном орудии горение пороха заканчивается до вылета снаряда из канала ствола. После сгорания пороха (l_k =0,75 l_g ) кинетическая энергия снаряда, продолжает возрастать за счет энергии, передаваемой при расширении пороховых газов. В момент вылета снаряда из ствола он имеет скорость υ_д (дульная скорость)

Несколько меньше начальной скорости снаряда на траектории-V₀ (на добавку полученную при действии пороховых газов на снаряд, вытекающих из канала ствола).

При решение задач внутренней баллистики весь процесс выстрела разбивают на четыре периода: предварительный, первый или основной, второй или период расширения пороховых газов, третий или период после действия. Предварительный период – от начала горения заряда до начала движения заряда. Предполагается, что воспламенитель сгорел мгновенно и зажжения пороха по всей поверхности произошло также мгновенно. Неучет воспламенительного периода выстрела (период воспламенения и период зажжение порохового заряда ) дает грубейшие ошибки в исследовании стабильности выстрела. С появлением быстродействующих ЭВМ проведены специальные внутрибаллистические исследования этого воспламенительного периода. За начало движения снаряда принят момент, когда ведущий поясок снаряда врезается на полную глубину нарезов ствола, то есть период врезания ведущего пояска в нарезы не учитывается. Предполагается, что порох в предварительном периоде горит в постоянном объеме, (пороховые газы не совершают работу). Давление газов в конце предварительного периода достигает величины Р₀ условно называемой давлением форсирования снаряда. Величина давления Р₀ может изменяться в широком диапазоне от нуля (мина) до 250-300 кг/см² (снаряд) и до 1000-1500 кг/см² (нуля). На рис. 1 этот период представлен участком 0- t₀ , где t₀- момент форсирования снаряда, кривая давления Р(t) на этом участке изображена отрезком кривой «a-b». В точке «a» Р= Рв

в точке «b» Р=Ро. Характер нарастания давления совпадает с кривой давления Р при постоянном объеме Wo=const.

Первый - основной период от момента форсирования снаряда до момента конца горения порохового заряда. Предполагается, что пороховой заряд состоит из одинаковых пороховых зерен, которые, зажигаясь одновременно и сгорают одновременно. Этот период – период горения пороха в увеличивающемся объеме заснарядного пространства. В начале этого периода, когда скорость снаряда еще невелика, объем образующихся газов растет быстрее, чем объем заснарядного пространства, в котором горит порох. В результате давление быстро повышается, достигая максимума – Рm, снаряд к этому моменту проходит путь – lm, скорость – υ_m. Давление Рm является важнейшей характеристикой данного орудия. Момент максимального давления соответствует условиям равенства объема газоприхода и объема прироста заснарядного пространства в следствии ускоряющегося движения снаряда (аналитический максимум dP/dt=0). В дальнейшем объем прироста заснарядного пространства идет быстрее, чем газоприход, давление постоянно уменьшается, так как снаряд движется с ускорением. В конце горения пороха давление Рк<Рm скорость снаряда Vк>Vm и путь снаряда lk>lm. На Рис.1 представлена кривая давления на участке to-t_k, момент достижения максимального давления обозначим t_m . В точке «b» кривая имеет «излом », что соответствует началу изменения заснарядного пространства (W₀= const). На рис. 2 представлена кривая давления пороховых газов при выстреле из миномета. Из Рис. 2 видно, что отсутствует предварительный период выстрела. Мина начинает двигаться при давлении газов воспламенителя. Пороховой заряд сгорает на восходящей ветви не достигнув аналитического максимума. Здесь на лицо физический максимум давления (Pm=Pk, dP/dt 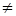0).

Второй или период расширения пороховых газов. Он начинается с момента конца горения пороха – t_k и заканчивается моментом вылета снаряда из ствола - t_g, когда дно снаряда проходит дульный срез ствола. В этом периоде несмотря на то, что горение порохового заряда отсутствует, давление пороховых газов, даже у дульного среза очень большое (Рд=800-1000 кг/см² ) и пороховые газы расширяясь, передают значительную часть своей энергии снаряду. Снаряд приобретает требуемую скорость –υ_д>υ_m.

На кривой давления – этот участок t_к-t_g (рисунок 1 и 2 ) в точке «К» кривая имеет «излом», который связан с прекращением газоприхода (в точке «К» dP/dt имеет разные значения как и в точке «b» ).

Третий или период последействия. Он начинается с момента вылета снаряда из канала ствола t_д и заканчивается моментом падения давления пороховых газов, вытекающих из канала ствола до давления Pn=1,8 кг/см² (0,18 МПа). На рисунке 1 этот период обозначен участком tд - tп. tп – момент окончания воздействия пороховых газов на ствол. Как правило, воздействие пороховых газов на снаряд заканчивается раньше. На рисунке 1 этот момент обозначен через tп, отрезок кривой обозначен пунктирной линией. В этот период снаряд достигает максимальной скорости – υ_max=υ₀. Прирост скорости небольшой υ=0,5-2% от υ_д. Однако, в этот период откатные части орудия приобретают основную часть энергии отката за счет истечения пороховых газов из ствола. Для уменьшения этой части энергии отката применяют дульный тормоз. В точке «д» кривая давления P(t) имеет "излом" т.к. заканчивается период расширения пороховых газов и начинается период истечения. Падение давления в этот момент идет быстрее.

Рисунок 1 - Кривая давления газов и скорости снаряда в функции времени.

Рис. 2 - Кривая давления газов и скорости мины в функции времени.

С термодинамической точки зрения орудие рассматривают как тепловую машину. В явлении выстрела тогда различают следующие основные процессы:

1. Горение пороха и образование газов, нагретых до очень высокой температуры и обладающих большим запасом внутренней энергии. В этом процессе скорость горения зависит в основном от природы и температуры пороха и от давления газов.

2. Преобразование тепловой энергии пороховых газов в кинетическую энергию движения системы - газы заряда - снаряд - ствол - лафет.

3. Движение газов заряда, снаряда и ствола.

Все эти процессы взаимосвязаны и протекают одновременно. Несмотря на высокую интенсивность быстропротекающих при выстреле из орудия процессов, они тем не имение закономерны, в определенных пределах управляемы и при сохранении одних и тех же условиях заряжания стабильны от выстрела к выстрелу. Эти особенности процесса выстрела непосредственно зависят от свойства бездымных порохов гореть закономерно параллельными слоями со сравнительно небольшой скоростью и это позволяет управлять явлением выстрела, т.е. так регулировать приток газов при горении пороха в канале ствола в зависимости от условий горения, что бы получать нужный закон развития давления и требуемую скорость при вылете его из канала ствола.

Итак, форма кривой давления и работа кривой давления зависит от условий заряжания или данных о заряжании, куда входят следующие параметры заряжания:

Вес снаряда и его тип – q., кг

Калибр орудия - d, мм или дм

Объем зарядной каморы - W₀, дм³

и ее формула

Поперечное сечение канала ствола с учетом нарезов S, дм²

Объем нарезной части канала (форма канала, характеристика нарезов) – W_нар, дм³

Длина пути снаряда по каналу – lд, дм

Вес порохового заряда - ω, кг

Энергетические характеристики пороха – f, кг дм/кг

Удельный вес пороха – δ, кг/дм³

Форма и размеры порохового заряда – 2е₁,

Коэффициент при скорости горения u, дм/сек:кг/дм

вес воспламенителя ω, кг

Давление форсирования снаряда – Р₀, кг/дм²

Основные задачи внутренней баллистики – (прямая задача) по заданным условиям заряжания (параметры перечислены выше) определить элементы выстрела: давленье - P(t) , скорость снаряда - V(t), путь снаряда - l(t), относительную часть сгоревшего порохового заряда 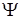(t) или относительную толщину сгоревшего слоя порохового зерна Z(t) как функция времени или как функции пути: P(l), υ(l), z(l), 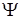(l), t(l). функции

Результаты решения прямой задачи являются основными и исходными при дальнейших расчетах ствола, лафета, снаряда, взрывателя, заряда, гильзы и т.д.

Вторая главная задача внутренней баллистики (обратная задача) - баллистическое проектирование орудия: определение конструктивных условий ствола и условий заряжания при которых снаряд данного калибра- d и веса -q получает при вылете из канала ствола заданную дульную скорость - υ_д. Задача имеет множество решений. Рассчитывают несколько вариантов и из них выбирают один - наиболее полно удовлетворяющий поставленным при проектировании тактико-техническим требованиям.

Для выбранного варианта орудия решается прямая задача внутренней баллистики, т.е. определяются P(t) и υ(t), а также P(l) и υ(l). Кроме этих главных задач имеются общие задачи внутренней баллистики как науки. К ним относятся:

1. Изучение и анализ условий и факторов, от которых зависит процесс выстрела из орудия.

2. Установление общих и частных теоретических и экспериментальных закономерностей, характеризующих и сопровождающих процесс выстрела.

3. Разработка методов решения задач, возникающих в процессе исследования выстрела.

4. Разработка специальной аппаратуры и специального оборудования для исследования явлений и процессов при выстреле.

5. Изыскание путей совершенствования и дальнейшего развития внутренней баллистики как науки, дающей научно-технические основы для ряда смежных артиллерийских дисциплин, проектирующих артиллерийские системы и боеприпасы к ним (сопротивление стволов, теория лафетов, проектирование снарядов, взрывателей и т.д.).

При решении сложных теоретических и практических задач внутренняя баллистика нередко прибегает к схематизации и упрощению изучаемых процессов , вводит определенные допущения, что позволяет решать задачи сначала в первом приближении, а затем уточнять полученные решения, учитывая влияние еще недостаточно изученных факторов. Для согласование расчетных данных с результатами опытов и стрельб вводятся коэффициенты согласования, характеризующие недостаточность наших значений исследуемых процессов и явлений.

При решении практических задач внутренняя баллистика пользуется следующими дисциплинами: физической химией, теорией взрывчатых веществ, термодинамикой, теоретической и технической механикой и математикой. Достижения в этих областях, особенно в вычислительной технике и приборостроении позволили внутренней баллистики сделать новый качественный скачок - создание средств метания с гиперзвуковыми скоростями (легко газовые и пороховые установки со скоростями 3000-8000 м/с).

Необходимо обратить внимание на то, что внутренняя баллистика - это, прежде всего опытная наука. Преимущественное значение имели эмпирические методы. В основу положено использование сравнительно простых формул, упрощенно выражающих полученную из опытов связь элементов выстрела (P,υ,T,l, 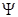, 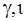) между собой. Эти формулы являются результатами опытных стрельб в различных условиях, причем входящие в них характеристики, и константы определяются из условий опыта и их можно применять именно в тех условиях и приделах, при которых они составлены. При решении внутри баллистических задач численными методами, в виду сложности явления выстрела не все его детали можно учесть даже приближенно, некоторые из них приходится откидывать при разработке математической модели выстрела, делать допущения о постоянстве некоторых параметров условий заряжания, вместо трехмерной задачи решать в постановке одномерной и т.д. и т.п. Поэтому уравнения внутренней баллистики дают лишь приближенные величины P,υ,l, 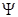,t. Для согласования с опытными данными вводятся коэффициенты согласования, которые можно применять в том диапазоне, в котором они получены. Например, опыты в манометрической бомбе при малых плотностях заряжания 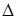=0,1-0,25 кг/дм³ показали, что импульс в конце горения пороха 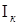, не зависит от плотности заряжания - 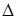и справедлив закон скорости горения 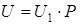. Перенося результаты I_k, полученные в манометрической бомбе в решение основной задачи внутренней баллистики орудия, где плотность заряжания 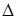=0,6-0,8 кг/дм³ мы получаем большие расхождения между опытными и расчетными значениями. На практике для согласования опытных и расчетных значений по давлению коэффициентом согласования выбирается 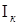, который зависит от типа орудия, его калибра, плотности заряжания и отличен от 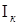полученного в манометрической бомбе при малых плотностях заряжания. Опыты по сжиганию пороха при больших плотностях заряжания 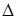=0,65 кг/дм³ проведенные Христенко Ю.Ф. в манометрической бомбе его собственной конструкции , показали большую разницу в 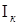при разных плотностях заряжания, что связано с запаздыванием изменения скорости горения при изменении давления , которое зависит от толщины «теплового слоя» и распределения температуры в нем, т.е. связанной с предысторией процесса.

Другой пример. Решение основной (прямой) задачи внутренней баллистики методом профессора Дроздова Н.Ф, которое имело широкое применение в модернизации советской артиллерии в настоящий момент является тормозом в создании орудий с гиперзвуковыми скоростями (более 2500 м/с). Этот метод базируется на квазиустановившемся течении порохового газа, что справедливо при малых скоростях снаряда, когда волновые процессы в газе невалируються, относительный вес пороха мал 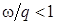. При скоростях снаряда 2500-3500 м/с, например, полученных Никулиным О.А на пороховых установках (ППН-23, ППН-34) на штатных порохах (ВТ, 4/7) по классической схеме выстрела, имеется существенное неустановившееся течение газа. Волновые процессы, происходящие в газе, при оптимальных условиях заряжания, перераспределяют его энергию в пользу снаряда. Эти оптимальные условия, полученные на основании решения прямой задачи внутренней баллистики с учетом волновых процессов (газодинамический метод) существенно отличается от условий полученных без учета волновых процессов (метод Дроздова Н.Ф - «термодинамический» метод который дает , можно сказать противоположные результаты). Этот пример, нисколько не умоляет заслуги Н.Ф Дроздова одного из основателя советской школы баллистиков. Метод Н.Ф Дроздова широко применяется в настоящие время при решении баллистических задач, например, стрелкового оружия. ПЭВМ позволяет с высокой точностью выдать результаты решения задачи в течении 3-5 минут. Однако, необходимо помнить о тех допущениях и насколько они справедливы при решении конкретной задачи и критически оценивать полученные результаты.

В настоящее время возможности вычислительной техники настолько выросли, что при решении баллистических задач можно отказаться от многих допущений и усложнить математическую модель выстрела (учесть воспламенительный период, отставание «пороховых зерен» изменение состава пороховых газов и т.д.). Однако, обязательна проверка полученных результатов на опытных стрельбах, на измерении необходимых параметров, что затруднительно из-за отсутствия необходимой аппаратуры. Иными словами отсутствие необходимых специальных приборов и аппаратуры сдерживает развитие баллистики как науки.

Из истории развития внутренней баллистики. История развития внутренней баллистики тесно связана с общим развитием физико-математических и технических наук, а также с развитием артиллерии.

Историю развития внутренней баллистики можно разделить на три этапа (условно). Первый этап накопление фактов (1742-1864 г.г.). В 1740 году Б. Робинс, изобретший баллистический маятник, написал работу «Новые принципы артиллеристской науки», в которой баллистика впервые была разделена на внешнюю и внутреннюю – 1742. Этап заканчивается изобретением «Ножа Родмана» для измерения давления.

На этом этапе развития необходимо отметить вклад ученых таких как Ж. Лагранжа, Д. Бернулли, Б. Робенса.

Основной целью внутрибаллистических исследований восемнадцатого века было определение начальных условий полета снаряда после вылета из пушки, а именно - определение дульной скорости. Кроме того ученые занимались выбором рациональных величин веса заряда, длины канала ствола и толщины стенок орудия.

Д. Бернулли наметил в этом вопросе подход основанный на анализе данных опытных стрельб. В 1727 году он провел большую серию опытных стрельб в Петербурге, измеряя время полета сферического снаряда при стрельбе вертикально вверх различными зарядами из пушек с различной длинной канала. Опыты Д. Бернулли привлекли внимание его друга и коллеги Л. Эйлера к вопросам баллистики, в том же 1727 году Л. Эйлер приступил к своему первому исследованию по баллистике.

Б. Робинс развил экспериментальный метод баллистических расчетов Бернулли. Как и Бернулли Робинс считал давление пороховых газов одинаковым всюду за снарядом (в данный момент времени) и подчиняющимся закону Бойля- Мариотта (Т=const). На основании более многочисленных и более достоверных экспериментальных данных, полученных с помощью весьма эффективного прибора - Баллистического маятника - Робинс пришел к результатам близким к выводам Д. Бернулли: зависимость скорости снаряда от длины канала у него была логарифмической. Баллистический маятник-приемник снарядов весом более 30 кг, отклоняющиеся на цепях при ударе.

Эйлер уточнил постановку задачи о движении снаряда в канале ствола по сравнению с постановкой Бернулли. Он указал на необходимость принимать во внимание некоторый объем пороха, не превращающегося в газ, а также на неточность закона Бойля- Мариотта в данном вопросе, предложив вместо него некоторое физическое соотношение между давлением и плотностью, установленное в его раннем исследовании упругой силы воздуха. Вместо введенной Д. Бернулли и используемой в восемнадцатом веке гипотезы мгновенного сгорания заряда, Эйлер предложил учитывать постепенность превращения пороха в газ, что было особенно важно для расчета действия новых сортов медленно горящих порохов. Наконец, Эйлер указал на необходимость учета движения массы пороховых газов. При этом он предлагал еще учитывать непостоянство плотности по координате в заснарядном пространстве. Все эти факторы Эйлер и пытался ввести в рассмотрение в своих баллистических исследованиях, ноне добился существенных успехов, поскольку еще не было достаточных экспериментальных , технических и физических предпосылок для этого.

Еще более уточнил постановку задачи внутренней баллистики Лагранж. Он четко сформулировал гипотезы намеченные Эйлером, облек их в математическую форму и записал исходные данные и начальные условия задачи. Кроме того, Лагранж наметил путь решения этой задачи при следующих предположениях:

1) пороховой заряд полностью превращается в газ до начала движения снаряда; газ имеет давление Р₀ и плотность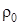

2) движение газа в канале ствола одномерным

3) зависимость давления от плотности газа имеет вид

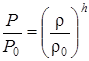, (1)

где Р- давление, 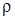- плотность, 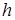- некоторый показатель

4) Используя соотношение падения плотности

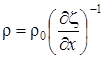, (2)

получаемое из закона сохранения массы, Лагранж записал дифференциальные уравнения движения :

газа 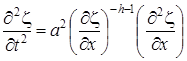, (3)

снаряда 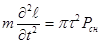, (4)

орудия 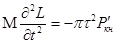, (5)

где 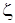-координата выбранного поперечного сечения газа в момент времени t; X- начальная координата, этого сечения;

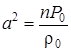;a- скорость звука в покоящемся газе;

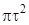- площадь поперечного сечения канала ствола;

l- путь пройденный снарядом;

L- путь пройденный стволом;

P_сн и P_кн - давление на дно снаряда и канала (х=0), соответственно;

m и M - масса снаряда и орудия, соответственно.

Начальные условия при t=0 ,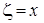

.

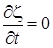
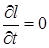
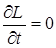Вместо системы уравнений (3)-(5) Лагранжем далее рассматривается следующие их интегралы. Закон сохранения количества движения:

. ,

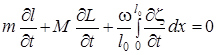и результат теоремы живых сил:

,

где 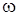-вес газа;

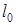- приведенная длина каморы - начальная длина каморы - начальная длина канала ствола, заполненная пороховым газом.

Далее Лагранж предпринял различные попытки аналитического решения поставленной задачи.

При допущении о независимости плотности от координаты Лагранж получил соотношение:

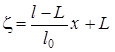
Т.е. линейный закон изменения скорости газа по длине канала ствола. При предположении о нулевом весе газа задача была решена аналитически.

Столь подробное описание постановки прямой задачи внутренней баллистики в трудах великих ученых математиков приведено, что бы показать насколько точно была поставлена задача. Задача Лагранжа была решена численно лишь через 200 лет спустя С.А Бетехтиным, Н.Н Поповым и новых относительных переменных О.А Никулиным.

На этом первом этапе развития баллистики стоит остановиться на решении основной задачи внутренней баллистики, выполненном французским ученым Р. Пиобером. Зависимость давления газа от плотности была более гибко и приспособлена реальным случаям постепенного, а не моментального сгорания заряда, как у Лагранжа. Обобщая большой опытный материал он предложил геометрическую теорию горения пороха (1839 год) и установил зависимость между плотностью пороховых зарядов и временем сгорания. Пиобер использовал эмпирическую формулу английского физика Б. Румфорда для зависимости давления от плотности, которую на основании опытных данных упростил и записал

где К- некоторая постоянная; 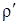-переменный множитель зависящей от времени и учитывающий полноту сгорания. h- показатели (из опытных данных. Пиобер определил границы изменения для n от 1,036 до 1,121).

К концу первого этапа относятся значительные успехи экспериментальной баллистики, выразившиеся в появлении двух основных приборов, которые широко применялся до настояшего времени: Хронограф Ле-Буланже для измерения скорости снаряда и крешер Нобля (1860 года) для измерения давления пороховых газов.

Отметим события в России, касающиеся артиллерии.1855 г- создание военной артиллерийской академии. 1857 г- опубликована первая теория горения пороха, созданная русским химиком Шишковым.