Свойства текучих материалов.

Для того, чтобы выбрать способ формования текучих материалов, необходимо иметь полную характеристику текучего материала.

Текучие массы - это тонкодисперсные системы (пылевидные сыпучие материалы, суспензии, коллоидные растворы с большим содержанием жидкой фазы).

Для оптимального проектирования необходимо знать закономерности воздействия рабочих органов, законы течения и структурно-механические свойства (вязкость, упругость, пластичность, характерная для ньютоновских и неньютоновских тел).

В зависимости от степенных характеристик текучести массы их относят к упругим, пластичным, вязкопластичным материалам.

Простейший реологический закон (реология - наука о течении вязких материалов):

T = K gⁿ (эта зависимость называется кривой течения)

Т - напряжение;

K, n - реологические константы;

g - скорость сдвига.

По виду приложения нагрузки структуру механических свойств текучих масс можно разделить на:

сдвиговые - поведение пищевых масс под действием сдвиговых и касательных напряжений;

компрессионные свойства - поведение продуктов в замкнутом объеме под действием внешнего напряжения;

поверхностные свойства - поведение продукта на границе раздела фаз под действием касательных и нормальных напряжений.

Кривая течения зависит от температуры (влияет на вязкость), от плотности содержания твердой фазы, от скорости.

Вид зависимости характеризует тип реологической модели материала.

Упругопластичные и прочностные свойства материала, определяющие закономерность изменения плотности от приложенного внешнего давления в замкнутом объеме, зависят от природы материала (кривая течения), от содействия твердой фазы и природы связки (жидкой фазы).

Поверхностные свойства характеризуются адгезионными и фрикционными свойствами (фрикция - внешнее трение), устанавливая связь приложенного напряжения от длительности предварительного контакта, а также от скорости отрыва.

Фрикционные свойства материала оцениваются по статическим и динамическим коэффициентам трения, по коэффициенту сопротивления скольжению (закон Кулона).

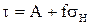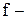, где коэффициент внутреннего трения; 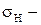внешнее напряжение