СИСТЕМЫ СЧИСЛЕНИЯ.
Саратовский государственный технический университет
СИСТЕМЫ СЧИСЛЕНИЯ
И ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
В ИНФОРМАЦИОННЫХ СИСТЕМАХ
Методические указания
к выполнению лабораторной работы
по курсу «Информатика»
для студентов специальности 071900
«Информационные системы и технологии»
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2005
ВВЕДЕНИЕ
Данные методические указания предназначены для выполнения лабораторных работ в рамках курса «Информатика» для студентов специальности ИСТ (071900). Целью работы является получение и закрепление знаний, полученных студентами при изучении курса «Информатика» путем выполнения самостоятельных заданий по темам: системы счисления, перевод между системами счисления и формамы представления чисел в информационных системах
СОДЕРЖАНИЕ РАБОТЫ
В рамках лабораторной работы студент выполняет задачи, которые приведены в методических указаниях.
СИСТЕМЫ СЧИСЛЕНИЯ.
1.1 Основные понятия и определения.
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
Все системы счисления делятся на позиционные и непозиционные.
Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе.
Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону.
Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления - "p".
В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.
Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:
N = anpn+an-1pn-1+ ... +a1p+a0+a-1p-1+a-2p-2+ ...
здесь N - число, aj - коэффициенты (цифры числа), p - основание системы счисления ( p>1).
Принято представлять числа в виде последовательности цифр:
N = anan-1 ... a1a0 . a-1a-2 ...
В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Точка опускается, если нет отрицательных степеней (число целое).
В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое - 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.
Двоичная система счисления.Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде:
N = bnbn-1 ... b1b0 . b-1b-2 ...
где bj либо 0, либо 1.
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1).
Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр - латинскими буквами: 10-A, 11-B, 12-C, 13-D, 14-E, 15-F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (табл. 1).
Таблица 1.
Наиболее важные системы счисления.
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||
| триады | тетрады | ||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
1.2 Перевод чисел из одной системы счисления в другую.
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
а) Перевести 10101101.1012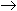 
"10" с.с.
10101101.1012 =1х27+ 0х26+ 1х25+ 0х24+ 1х23+ 1х22+ 0х21+ 1х20+ 1х2-1+ 0х2-2+ 1х2-3 = 173.62510
б) Перевести 703.048 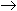"10" с.с.
703.048 = 7х82+ 0х81+ 3х80+ 0х8-1+ 4х8-2 = 451.062510
в) Перевести B2E.416 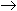"10" с.с.
B2E.416 = 11х162+ 2х161+ 14х160+ 4х16-1 = 2862.2510
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести 18110 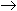"8" с.с.
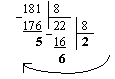
Результат: 18110 = 2658
б) Перевести 62210 "16" с.с.
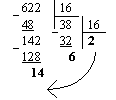
Результат: 62210 = 26E16
Дата добавления: 2015-08-01; просмотров: 815;