Линия рынка капитала. Рыночная линия ценной бумаги

Точка М обозначает рыночный портфель, r_f – безрисковая ставка доходности. Эффективные портфели находятся вдоль прямой, которая получила название «линия рынка капитала» (CML).

Уравнение CML имеет вид:

R_p = a ´ r_f + (1 – a) ´ R_m,

σ_p = (1 – a) ´ σ_m,

где: а – доля безрисковых ценных бумаг в портфеле; R_m, σ_m – доходность и среднеквадратичное отклонение рыночного портфеля; R_p, σ_p – доходность и среднеквадратичное отклонение эффективного портфеля.

Это уравнение может быть преобразовано следующим образом:

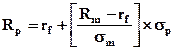(25.1).

Свойства линии CML:

1. R_p = f (σ_p) – линейная функция.

2. На линии рынка капитала расположены все эффективные портфели рынка.

3. Наклон линии рынка капитала определяется отношением: (Rm – r_f ) / σ_m.

4. В случае равновесия на рынке ЦБ все инвесторы будут стремиться иметь портфель M.

5. Доходность портфеля будет расти при увеличении в портфеле ЦБ с повышенным риском.

Ординату точки пересечения CML с вертикальной осью (безрисковая ставка) часто обозначают как награда за ожидание. Наклон CML называют наградой за единицу принятого риска. Таким образом, эти две величины можно интерпретировать как цены времени и риска.

Очевидно, что если линия безразличия какого-то инвестора касается CML в точке М, то он и выберет портфель М. Если уровень риска, характеризующийся величиной σ_m, его не устраивает, он может инвестировать часть своих средств в покупку безрисковых активов, имеющих норму отдачи r_f. Как правило, безрисковыми ценными бумагами являются краткосрочные государственные обязательства. Покупка этих активов представляет собой предоставление денег государству в долг. Портфель этого инвестора будет располагаться на участке r_fМ линии CML. Этот участок характеризует портфели всех инвесторов, дающих деньги в долг. Участок линии MG характеризует портфели инвесторов, склонных к повышенному риску.

Для осуществления рискованных инвестиций (R_p > R_m) они занимают деньги по пониженной ставке (R_p < R_m). Таким образом, участок MG линии CML характеризует портфели инвесторов, занимающих деньги.

Поскольку эффективный портфель состоит из N ценных бумаг, уравнение (25.1) справедливо для любой ценной бумаги, имеющейся на рынке. Это дает возможность построить рыночную линию ценной бумаги (SML).

Уравнение SML имеет вид: r_i = r_f + (R_m – r_f) ´ b_i,

где: r_i – доходность i-й ценной бумаги; r_f – безрисковая ставка; R_m – доходность рыночного портфеля; b_i – коэффициент наклона линии SML.

.

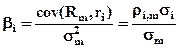Разность (R_m – r_f) ´ b_i характеризует премию за систематический риск, то есть риск, возникающий в результате колебаний доходности на всем рынке ценных бумаг.

Для практических целей R_m можно рассматривать как доходность, зарабатываемую на хорошо диверсифицируемом портфеле. Коэффициент b_i измеряет реакцию R_m на i-ю ценную бумагу.

Акция, которая имеет доходность, являющуюся зеркальным отражением доходности рыночного портфеля М имеет b = 1. Такие акции называются «нейтральными».

Акции со значением b > 1 называются «агрессивными». Они повышаются в цене быстрее, чем рыночная цена в целом (но и падают быстрее).

Акции со значением b < 1 называются «защищающимися».

Общий риск ценной бумаги i состоит из двух частей:

– рыночный (систематический) риск – s_i^S;

– собственный (несистематический) риск – s_i^NS.

s_i = s_i^S + s_i^NS; s_i = s_m ´ b_i + s_i*,

где: s_i* – собственный риск ценной бумаги.

Диверсификация портфеля приводит к усреднению рыночного риска, но не снижает его.

Собственный риск снижается при диверсификации портфеля. Как следствие снижается общий риск портфеля.

Дисконтирование и компаундирование. Простые и сложные проценты. Аннуитет. Понятие эффективной ставки процента. Расчет текущей и будущей стоимости потоков пренумерандо и постнумерандо