И главного момента сил инерции

Найдем главный вектор и главный момент сил инерции СМТ, совершающей любое движение. Сравнивая соотношение (5.3) с третьим соотношение (4.17) из теоремы о движении центра масс и соотношение (5.5) с соотношением (4.24) из теоремы об изменении кинетического момента, получим:

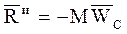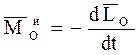, . (5.6)

Найдем главный момент сил инерции СМТ для частного случая – вращательного движения НМС относительно неподвижной оси z. Спроектировав соотношение (5.5) на ось z и сравнивая его с третьим соотношением (4.25) теоремы об изменении кинетического момента СМТ, можно записать:

.

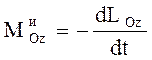Подставив в это соотношение выражение для кинетического момента НМС, вращающейся относительно неподвижной оси z (4.28), получим выражение для главного момента сил инерции НМС, вращающейся относительно неподвижной оси:

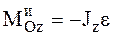. (5.7)