Количества движения МТ
Умножим векторно слева обе части основного закона динамики – соотношение (1.1) на радиус-вектор 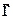 (рис. 11):
(рис. 11):
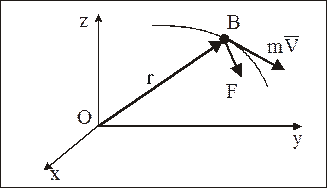
Рис. 11
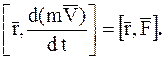 (1.33)
(1.33)
Преобразуем левую часть, представив ее в виде тождества:
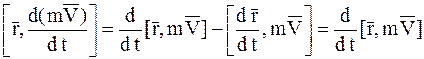
(так как 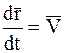 , то
, то 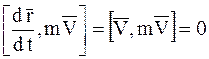 ).
).
Соотношение (1.33) примет вид:
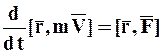 . (1.34)
. (1.34)
Введя обозначение момента количества движения МТ относительно центра О через вектор 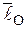 , получим:
, получим:
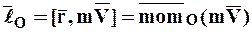 . (1.35)
. (1.35)
Соотношение (1.34) с учетом (1.35) и того, что его правая часть есть момент силы относительно центра О: 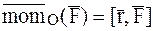 , примет вид:
, примет вид:
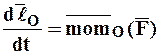 . (1.36)
. (1.36)
Соотношение (1.36) выражает теорему об изменении момента количества движения МТ в векторной форме.
Теорема: Производная по времени от момента количества движения МТ относительно какого-либо центра равна моменту силы, действующей на МТ, относительно того же центра.
Проектируя равенство (1.36) на оси декартовой системы координат, получим эту теорему в скалярной форме:
 ,
,
 , (1.37)
, (1.37)
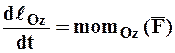 .
.
Здесь lOx, lOy, lOz – проекции момента количества движения МТ на оси декартовой системы координат (моменты количества движения МТ относительно координатных осей), а 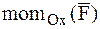 ,
, 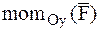 ,
, 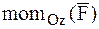 , – моменты силы относительно координатных осей.
, – моменты силы относительно координатных осей.
Теорема: Производная по времени от проекции момента количества движения МТ на какую-либо ось равна моменту силы, действующей на МТ, относительно той же оси .
Следствия: если 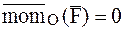 , то
, то 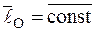 , т. е. МТ движется таким образом, что момент количества движения МТ остается постоянным;
, т. е. МТ движется таким образом, что момент количества движения МТ остается постоянным;
если 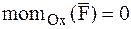 , то
, то 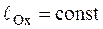 , т. е. МТ движется таким образом, что проекция момента количества движения МТ на осьхостается постоянной.
, т. е. МТ движется таким образом, что проекция момента количества движения МТ на осьхостается постоянной.
Первое из полученных соотношений представляет собой закон сохранения момента количества движения МТ.
Дата добавления: 2015-08-01; просмотров: 575;
