В призматическом русле

Допустим, что имеется некоторый участок потока, движущегося в призматическом русле с горизонтальным дном; предположим, что на этом участке наблюдается гидравлический прыжок (рис.18.1). Выделим из потока некоторый объем, ограниченный сечениями, в которых глубины равны h₁ и h₂. Применяя к выбранному отсеку уравнения сохранения количества движения, получим основное уравнение гидравлического прыжка

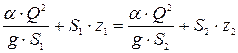. (18.1)

В этом уравнении Q – расход, одинаковый для сечений до и после прыжка; S₁ и S₂ – площади живых сечений с глубинами h₁ и h₂; z₁ и z₂ – глубины погружения центров тяжести сечений S₁ и S₂; g – ускорение свободного падения; α – коэффициент, численно равный 1,05. Уравнение (18.1) связывает гидравлические элементы потока до и после прыжка, обращает на себя внимание симметричностью вида левой и правой частей.