Полосы равного наклона

Из формулы (10) следует, что оптическая разность хода D лучей, а, следовательно, и результат интерференции в тонких пленках, определяются четырьмя величинами – l, d, п и i. В зависимости от того, какая из величин – i или d – является переменной, различают полосы равного наклона и равной толщины.

Пусть плоскопараллельная пластина толщиной d освещается рассеянным монохроматическим светом от точечного источника S (рис. 4).

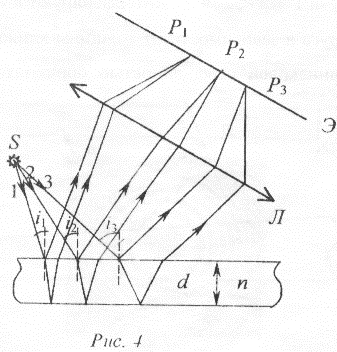
Рассмотрим три луча 1, 2 и 3, плоскость падения которых совпадает с плоскостью рисунка, а углы падения равны соответственно i₁, i₂ и i₃ При отражении от верхней и нижней поверхности пластины лучи интерферируют в точках Р₁, Р₂ и Р₃, усиливая или ослабляя друг друга в зависимости от угла падения. Такие же точки образуют лучи, лежащие в других плоскостях падения. Совокупность точек с одинаковой освещенностью дают на экране интерференционные полосы в виде концентрических эллипсов. Поскольку каждая из таких полос образована лучами, падающими на пластину под одним и тем же углом (под одинаковым наклоном), то они называются полосами равного наклона. При освещении пластины белым светом полосы имеют радужную окраску.

Лучи, отразившиеся от верхней и нижней граней плоскопараллельной пластины, параллельны друг другу и «пересекаются» в бесконечности. Поэтому го­ворят, что полосы равного наклона локализованы в бесконечности. Их можно наблюдать невооруженным глазом, если аккомодировать его на бесконечность.