Распределение совокупного дохода по 20%-ным группам населения
| Группа населения | Денежные доходы, в % | ||||
| 1991 г. | /992 г. | 1993 г. | 1994 г. | 1995 г. | |
| Первая (с наименьшими | |||||
| доходами) | 11,9 | 6,0 | 5,8 | 5,3 | 5,5 |
| Вторая | 15,8 | 11,6 | 11,1 | 10,2 | 10,2 |
| Третья | 18,8 | 17,6 | 16,7 | 15,2 | 15,0 |
| Четвертая | 22,8 | 26,5 | 24,8 | 22,4 | |
| Пятая (с наибольшими | |||||
| доходами) | 30,7 | 38,3 | 41,6 | 46,3 | 46,9 |
| Итого | 100,0 | 100,0 | 100,0 | 100,0 | 100,0 |
Источник: Социальная статистика: Учебник. С. 96.
сравнению с низкодоходными группами населения. Различают коэффициент фондов (соотношение между средними значениями доходов внутри сравниваемых групп населения или их долями в общем объеме доходов) и децильный коэффициент дифференциации (отношение уровней доходов, ниже и выше которых находятся десятые доли совокупности в разных концах ряда распределения населения по уровню среднедушевых денежных доходов). Например, если в 1993 г. соотношение доходов 10% наиболее и наименее обеспеченного населения составляло 11,2 раза, то в 1994 г. оно возросло до 15,1 раза, в 1995 г. оно несколько снизилось (до 13,5 раза)[385].
Показатели дифференциации охватывают и коэффициенты концентрации доходов Лоренца и Джини. Они относятся к системе оценок, известной как методология Парето—Лоренца—Джини, широко используемой в зарубежной социальной статистике. Итальянский экономист и социолог В. Парето (1848-1923) обобщил данные некоторых стран и установил, что между уровнем доходов и числом их получателей существует обратная зависимость, названная в литературе законом Парето. Американский статистик и экономист О. Лоренц (1876—1959) развил этот закон, предложив его графическое изображение в виде кривой, получившей название “кривая Лоренца” (схема 10.1).
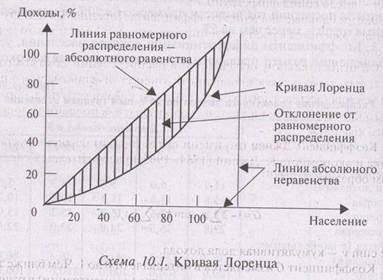
Кривая Лоренца представляет собой кривую концентрации отдельных элементов статистической совокупности по группам. На графике Лоренца в случае равномерного распределения дохода попарные доли населения и доходов должны совпадать и располагаться на диагонали квадрата, что и означает полное отсутствие концентрации дохода. Отрезки прямых, соединяющих точки, соответствующие накопленным частям и нарастающим процентам дохода, образуют ломаную линию концентрации (кривую Лоренца). Чем больше эта линия отличается от диагонали (чем больше ее вогнутость), тем больше неравномерность распределения доходов, соответственно выше его концентрация.
Коэффициент Лоренца как относительная характеристика неравенства в распределении доходов определяется по формуле
|y1 – x1| + |y2 – x2| + |y3 – x3| +…+|yn – x n| = Σ(|yi – xi |) ,
2 2
где уi - доля доходов, сосредоточенная у i-й социальной группы населения;
хi — доля населения, принадлежащая к i-й социальной группе в общей численности населения;
п - число социальных групп.
Экстремальные значения коэффициента Лоренца: L = 0 в случае полного равенства в распределении доходов, L = 1 при полном неравенстве.
Об относительном неравенстве в распределении дохода может свидетельствовать доля площади отклонения от равномерного распределения (абсолютного равенства), т.е. площади сегмента, образуемого кривой Лоренца и диагональю квадрата, в половине площади этого квадрата.
Коэффициент Джини (по имени его автора, итальянского статистика и экономиста К. Джини (1884—1965)) рассчитывается следующим образом:
n n
G = 1 – 2 Σ xi cum yi + Σ xi yi ,
i = n i = n
где cum у i — кумулятивная доля дохода.
Коэффициент G изменяется в интервале от 0 до 1. Чем ближе значение G к 1, тем выше уровень неравенства (концентрации) в распределении совокупного дохода; чем ближе он к 0, тем выше уровень равенства (табл. 10.11).
Таблица 10.1]
Дата добавления: 2015-08-01; просмотров: 1359;
