Эктонная модель катодного пятна

Эктон описывается как кратковременный процесс выброса плазмы с поверхноси микроучастка катода. В результате такого процесса вакуумный разряд обеспечивается носителями электрического тока. В процессе взрыва микроучастка катода образуется облако сверхплотной (около 10 ²² см^-3) плазмы. Сам этот процесс взрыва может быть описан несколькими способами

Тепловая модель эктона

Основным уравнением тепловой модели является уравнение теплопроводности записанное для случая сферической симметрии

( 6.10)

Начальные и граничные условия Tôt = 0 = T0, Tôr¥® = T0;

Условия на границе расплав-твердое тело T(rпл, t) = Tпл, lÑTôT = - lÑTôЖ = rvплwпл;

Условия на границе металл-плазма

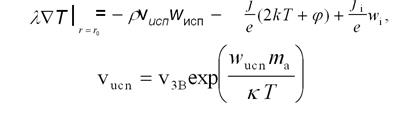
r - плотность материала катода; c - удельная теплоемкость; l - коэффициент теплопроводности; i - ток, переносимый через эмиссионный центр на катоде; - плотность электронного тока; q - угол при вершине острия (см. рис. 7.1); ji - плотность ионного тока на поверхности; wi - энергия, приносимая ионом на поверхность катода; e - заряд электрона; k = k0T - удельное сопротивление катода; T0 - начальная температура; rпл, vпл, wпл - радиус, скорость и удельная теплота плавления; r0, vисп, wисп - радиус, скорость и удельная теплота испарения; vзв - скорость звука (поперечная) в металле; ma - масса атома вещества катода; j - работа выхода катода; индексы “т” и “ж” указывают на граничные условия в месте раздела твердой и жидкой фаз. Величины r, c, l считалисьне зависящими от температуры и одинаковыми для жидкой и твердой фаз. Ток задавался линейно растущим со временем или постоянным. Движением жидкости под действием давления плазменной струи пренебрегалось.

Уравнение эмиссии

i = 2pr02(1 - cos q/2)AT2exp(j-/kT),

Где работа выхода вычисляется с поправкой Шоттки j = j0 - jD

Где поправка Шоттки Dj = (e3E)1/2,

Напряженность поля вычисляется по той же формуле Маккоуна что и для стационарных моделей

Расчеты показали, что эмиссия электронов начинается, существует короткое время, а затем исчезает из-за охлаждения эмиссионного центра. Этот кратковременный выброс электронов мы и назвали эктоном. Время существования эктона te сильно зависит от величины тока (см. табл. 7.1). Время te = 0,4 нс при токе 10 А является очень коротким и не соответствует экспериментальным данным, т.к. время цикла вакуумной дуги для медного катода обычно ~ 10-8 с. Это объясняется тем, что катодное пятно дуги обычно существует на микровыступах катода, а время te ~ q -4, где q - угол вершины конуса. Поэтому фактическое время жизни эктона значительно больше. Однако первичный эктон, возбужденный, например, мощным лучом лазера на абсолютно плоской поверхности при токе в несколько ампер, будет иметь te << 1 нс.

Самопроизвольное погасание дуги

Внутренняя неустойчивость процесса функционирования вакуумной дуги лежит в самой основе эктонной модели. На ее базе мы дали анализ явления самопроизвольного погасания дуги . Причиной этой неустойчивости является конечное время жизни эктона и связанная с этим цикличность процессов в катодном пятне вакуумной дуги. В основе эктонной модели лежит предположение, что катодное пятно вакуумной дуги состоит из отдельных ячеек. Каждая ячейка переносит ток, который не превышает удвоенного значения порогового тока iп. Ячейка имеет конечное время жизни tц, которое называется циклом. Цикл состоит из двух стадий: первая стадия - это время te, в течение которого происходит непосредственное функционирование эктона, и вторая стадия меньшей длительности ti, в течение которой происходит инициирование нового эктона взамен исчезнувшего.

Вероятность того, что эктона нет, равна a, то есть

a = ti /(te + ti),

а то, что он есть

b = 1 - a = te/(te + ti),

Величина a характеризует эффективность восстановительного механизма. Если ток дуги менее 2iп - двух пороговых токов, то в катодном пятне будет одна ячейка, в которой то исчезает, то возникает новый эктон. При i >> iп количество ячеек

L = i/2iп.

где tс - длительность цикла. Определим момент погасания дуги как таковой, когда не функционирует ни одного эктона

Тогда вероятность погасания дуги в момент времени т равна

Так как aL << 1 при l >> 1, то используя разложение экспоненты в ряд Тейлора получим

w = exp(-taL/tц).

Cледовательно, из N0 дуг, зажженных к моменту времени t, горят

N = N0exp(-taL/tц).

Это совпадает по форме с эмпирически установленным соотношением, где величина

t = tц/aL

является средним временем горения дуги.