Стационарная модель катодного пятна
Стационарные модели или эрозионно-эмиссионные катодного пятна имеют следующие общие черты. Раз модель стационарна , значит движение границ испарения и расплава не должно учитываться. Следовательно модель должна быть одномерной. Ток пятна обеспечивается эмиссией электронов на границе металл-плазма. Поступление материала в разрядный промежуток обеспечивается испарением с границы металл-вакуум.
Качественное описание
Кратко сценарий функционирования катодного пятна можно записать следующим образом : Неподвижное или медленное перемещающееся катодное пятно на поверхности металла представляет собой сильно нагретую область. Благодаря высокой температуре металл в этой области испаряется, образуя струю пара, истекающую в межэлектродное пространство, давление в котором близко к нулю. Высокая температура поверхности в пятне поддерживается за счет энергии, которая приносится в. основном ионами, поступающими из прикатодной плазмы на поверхность электрода. В стационарных усло-
виях эта энергия расходуется на компенсацию различного рода потерь (отвод тепла в тело электрода теплопроводностью; потери на излучение; потери энергии, связанные с эмиссией электронов, и т. д.) и на генерацию необходимого количества пара. Вблизи поверхности металла в области порядка длины свободного лробега иона (lt ~ 10~5—10~6 см) формируется слой объемного заряда, в котором имеет место существенное (~10 в) падение потенциала (катод- ное падение) и сильные (~106—107 в/см) электрические поля. Этот слой является основным источником энергии, обеспечивающим существование
лятна. Ионы прикатодной плазмы ускоряются в слое объемного заряда ΉΟ направлению к поверхности электрода, приобретая кинетическую энергию, которую они передают при столкновении поверхности металла. Эта энергия вместе с энергией, выделяющейся при нейтрализации иона, и составляет основной приток энергии к поверхности металла. С другой стороны, благодаря высокой температуре поверхности электрода в пятне и сильному электрическому полю в слое объемного заряда, электрод эмиттирует электроны. Эти электроны ускоряются в слое объемного заряда и образуют высокоэнергетический пучок, поступающий в прика- тодную плазму. Энергия, приносимая в прикатодную плазму эмиттированными электронами, расходуется в зоне релаксации пучка на ионизацию и нагрев компонент плазмы. Физические процессы и динамика области релаксации определяют, в частности, ионный поток на поверхность электрода. Протя-
женность зоны релаксации пучка (или зоны ионизации) определяется параметрами плазмы (1р ~ 104—10"3 еж), но благодаря высокому давлению пара вблизи электрода и большому сечению столкновений ион — атом она оказывается много больше длины свободного пробега иона, а следо- вательно, и много больше протяженности слоя объемного заряда. За счет этого напряженность электрического поля в зоне релаксации относительно мала. За зоной релаксации простирается широкая область собственно
струи, в которой имеет место течение многокомпонентной плазмы.
Основные формулы
Плотность тока электронной эмиссии
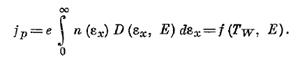
Здесь е — заряд электрона, T-w — температура поверхности металла в пятне, η (бж) —
плотность состояний электронов металла, D (гх, Е) — коэффициент прозрачности потенциального барьера на границе металла, Ε — средняя величина нормальной
поверхности электрического поля
Электрическое поле считается по формуле Маккоуна (эта формула описывает поведение напряженности электрического поля Е в слое плазмы , окружающей металл)
Уравнение Маккоуна для падения напряжения на слое.
|
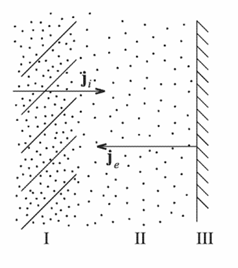
| Катодный плазменный слой. I- квазинейтральная плазма, II – Область объемного заряда, III -термокатод |
Рассматривается одномерный случай бесстолкновительной плазмы. Термокатод является неограниченно эмиттируюшим. Катод с плоскости x=0 эмиттирует ток холодных электронов плотностью je. Из плазмы на катод падает поток холодных ионов плотностью ji. Потоком электронов из плазмы пренебрегаем. Начальные скорости электронов и ионов предполагаем равными 0.
Граничные условия Eôx ® ¥ = 0, Fôx¥® = U; F(0)=0
Уравнения для концентрации ионов и электронов получены из выражения для плотности тока j=nve. Скорость задается потенциалом приобретаемым частицей при движении от границы задачи.
 |
Подставляем эти значения в уравнение Пуассона получаем
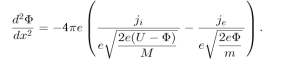 |
После интегрирования по х
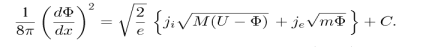
Постоянную С получаем из учета граничных условий. Получается формула Маккоуна для катодного падения
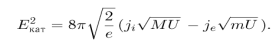
При этом данная формула не дает удовлетворительных значений катодного падения.
Процесс испарения (эрозии) описывается системой уравнений баланса потоков энергии различной природы. Чаще всего размер пятна искусственно ограничивается неизменным радиусом r.
Для потока тепла отводимого теплопроводностью
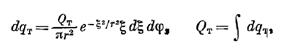
где gT, QT — плотность и суммарный приток энергии, отводимые теплопроводностью, ξ, φ — цилиндрические координаты.
Энергия, передаваемая поверхности электрода в области катодного пятна, пределяется в основном энергией ионов, которая складывается из их кинетической энергии и энергии, выделив- шейся при нейтрализации) :
1 = U We +Vt- φ*), Q = nr*q;
здесь Uι — потенциал ионизации атомов металла, φ* — эффективная работа выхода.
И, наконец, разница подводимой и оводимой энергии на катод тратится на испарение вещества катода излучение поверхности эмиссию электронов итд
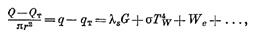
где q — средний поток тепла (энергии) к единице поверхности пятна,
λ8 — теплота испарения, σ — постоянная в законе Стефана — Больцмана, G — плотность потока испаренного вещества, We – поверхностные потери на эмиссию электронов.
Представленная система уравнений нуждается во внешних задаваемых параметрах в частности размере пятна u и общем токе через пятно I
Стационарная модель не в состоянии объяснить нестабильность горения дуги и ее внезапные обрывы
Дата добавления: 2015-07-30; просмотров: 1658;
