Расчет режима максимальных нагрузок

Расчет режима максимальных нагрузок выполняется методом последовательных приближений. В качестве первого приближения (на первом этапе расчетов) принимается, что напряжения в узлах равны номинальному напряжению. При данном условии находятся мощности в конце и начале каждого участка схемы замещения сети с учетом потерь мощности в продольных сопротивлениях, зарядных мощностей линий электропередачи Q_c и потерь в стали трансформаторов 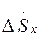. Потери мощности 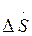и зарядные мощности Q_c определяются по U_ном. На втором этапе расчетов по найденным значениям мощностей и напряжению базисного узла находятся напряжения в узлах с учетом потерь напряжения в линиях и в трансформаторах. Ниже рассмотрено применение метода последовательных приближений для расчета параметров режима электрической сети, схема замещения которой изображена на рис. 3.1.

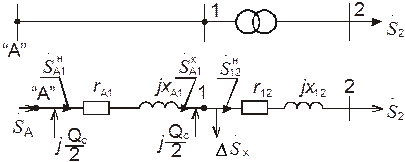
Рис. 3.1. Фрагмент электрической сети и ее схема замещения

Исходными данными являются параметры схемы замещения линии электропередачи 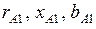, сопротивления схемы замещения двухобмоточного трансформатора 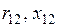, потери холостого хода 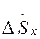, мощность нагрузки в узле 2 - 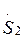и напряжение базисного узла .

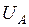Необходимо определить мощность 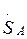, отдаваемую в сеть, и напряжения в узлах 1 и 2.

Потери мощности в сопротивлениях схемы замещения трансформатора рассчитываются по мощности нагрузки:

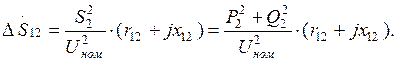(3.2)

Мощность 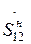, поступающая в обмотки трансформатора, больше мощности нагрузки 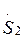на величину :

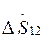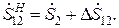(3.3)

Мощность в конце линии 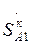определяется по первому закону Кирхгофа для узла 1:

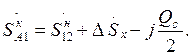(3.4)

Мощность в начале линии 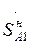отличается от мощности в конце на величину потерь мощности в сопротивлениях линии:

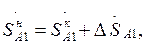(3.5)

.

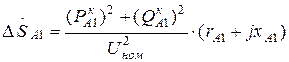Мощность, отдаваемая источником, равна

.

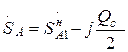Далее, используя найденные значения мощностей в начале каждой ветви и напряжение в начальном узле, определяют напряжение в следующем узле, например, для узла 1:

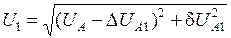; (3.6)

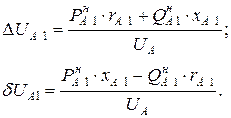(3.7)

Для сети напряжением 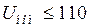кВ поперечную составляющую падения напряжения допускается не учитывать, т.е. потеря напряжения приравнивается продольной составляющей падения напряжения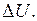

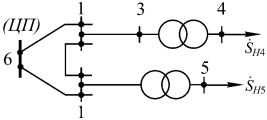
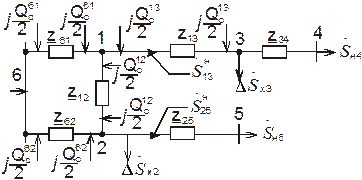
Если спроектированная электрическая сеть имеет замкнутую часть, то для упрощения вводится понятие расчетной нагрузки. На рис. 3.2, а изображена расчетная схема замкнутой электрической сети, состоящая из четырех линий электропередачи и двух трансформаторных подстанций, а на рис. 3.2, б - ее схема замещения.

Для того, чтобы упростить схему замещения, на участках 1-3-4 и 2-5 рассчитываются потоки мощности с учетом потерь мощности по формулам (3.2) – (3.5). Далее определяются расчетные мощности узлов 1 и 2:

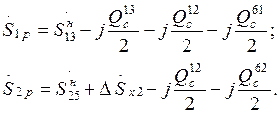(3.8)

а)

б)

Рис. 3.2. Расчетная схема и схема замещения замкнутой сети

Используя значения 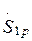и 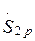, замкнутую часть схемы можно представить в виде линии с двухсторонним питанием (рис. 3.3).

Рис. 3.3. Упрощенная схема замещения с расчетными нагрузками

Далее расчеты производятся в следующей последовательности.

1. Произвольно задаются направлением потоков мощности в ветвях

упрощенной схемы замещения.

2. Определяются потоки мощности и в линиях, отходящих от центра питания (узла 6):

(3.9)

где - сопряженный комплекс сопротивления.

3. Мощности на остальных участках (в данной сети – на участке 12) определяются на основании первого закона Кирхгофа, последовательно примененного для каждого узла схемы замещения. Так как на данном этапе расчет ведется без учета потерь мощности, то мощности в конце каждой ветви и в ее начале равны.

4. Линия с двухсторонним питанием "мысленно разрезается" по точке раздела мощностей (точке, к которой мощности поступают с двух сторон, в рассматриваемом примере это узел 2). В конце участка 1-2 прикладывается мощность 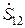, а в конце участка 6-2 мощность .

5. Рассчитываются потоки мощности в ветвях 6-1-2 и 6-2 и напряжения в узлах методом последовательных приближений, как это делалось для разомкнутых сетей.

Для того чтобы не загромождать пояснительную записку однотипными расчетами, целесообразно, показав ход расчета на конкретном примере, свести результаты в таблицы, параметры режима нанести на схему замещения.