Диаграмма 5

Рис.2. (окончание) Диаграммы, поясняющие процесс образования p-n перехода

Ширина p-n перехода может быть найдена при интегрировании уравнения Пуассона, которое определяет распределение напряженности электрического поля E(x) и потенциала j(x). При этом получают:

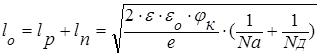
где e - диэлектрическая проницаемость полупроводника; e_о - диэлектрическая проницаемость вакуума (электрическая постоянная); e – заряд электрона; j_К - контактная разность потенциалов; Nа - концентрация акцепторов; Nд - концентрация доноров.

Так как Nа>>Nд, то l_p<<l_n, и приближенно можно записать

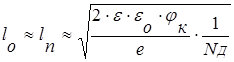
Распределение напряженности электрического поля и потенциала в p-n переходе (диаграммы 4 и 5 рис. 2) получают из решения уравнения Пуассона.

При увеличении концентрации примеси возрастает максимальное значение напряженности электрического поля в p-n переходе. Электрическое поле препятствует переходу основных носителей заряда через p-n переход. При контакте двух полупроводников возникает потенциальный барьер и распределение потенциала вдоль p-n перехода показано на диаграмме 5 рис. 2. j(x) также получается путем двойного интегрирования уравнения Пуассона. Причем функция j(x) состоит из двух параболических участков, поскольку она получена интегрированием кусочно-линейной функции E(x) и имеет точку перегиба при x=0. Высота потенциального барьера в равновесном состоянии равна контактной разности потенциалов j_к:

,
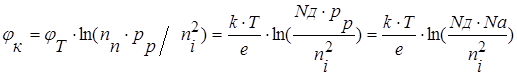так как p_p=n_i+Nа»Nа, Nа>>n_{i (} n_i=p_{i ! )}.

Контактная разность потенциалов зависит от температуры окружающей среды. С увеличением температуры контактная разность потенциалов уменьшается. Это связано с тем, что в выражении для j_к с увеличением температуры окружающей среды возрастает значение температурного потенциала j_Т, но 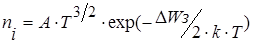также возрастает и это увеличение происходит быстрее, чем рост температурного потенциала, поэтому контактная разность потенциалов при увеличении температуры уменьшается.