Компиляторы. Лексический анализ. Преобразования грамматик.

Для грамматик, например леволинейного типа, существует алгоритм определения того, принадлежит ли анализируемая цепочка языку, порождаемому этой грамматикой. Алгоритм заключается в слудйющем: 1-й символ исходной цепочки a1a2a3a….an# заменяетися нетерминальным символом А, для которого в грамматике есть правило вывода A->ai, т.е. производится свертка терминала a1 к нетерминальному A. Затем многократно до тех пор, пока не считан признак конца цепочка, выполняется следующие шаги. Полученный на предыдущем шаге нетерминал A и расположенный непосредственно справа это него очередной терминал ai исх цеп, заменяется нетерминалом B, для которого в грамматике есть правило вывода вида B->Aai. Это эквивалентно построению дерева разбора методом снизу вверх. При работе алгоритма возможны слуд ситуации:

1. Прочитана вся цепочка, на каждом шаге находилась единственная нужная свертка, на последнем шаге свертка произошла к символу S. Это значит, что цепочка принадлежит языку. a1a2a3…an#ЄL(G).

2. Прочитана вся цепочка. На каждом шаге находилась единственная нужная свертка, на последнем шаге – свертка произошла к символу, отличному от S. Это означает, что исх цепочка не принадлежит языку a.

3.На некотором шаге не нашлаось нужной свертки, т.е. для полученного на предыдущем шаге нетерминала A и расположенного непосредственно справа от него очередного терминала ai исх цепочки, не нашлось нетерминала B, для которого в грамматикае было бы правило вывода B->Aai. Это означает, что исх цепочка не принадлежит языку.

4. На некотором шаге работы алгоритма оказалось, что есть более одной подходящей свертки, т.е. в грамматике разные нетерминалы имеют правила вывода с одинаковыми правыми частями и поэтому не понятно к которому из них производить свертку. Это говорит о недетерминированности разбора. Для того, чтобы при лексическом разборе быстрее находить правила с подходящей правой частью фиксируют все возможные свертки в описании грамматики. Это определяется только грамматикой и не зависит от вида анализируемой цепочки.

Диаграмма определяет конечный автомат, построенный по регулярной грамматике, который допускает множество цепочек составляющих язык, определяемый этой грамматикой. Среди всех состояний выделяются начальные и конечные. По мере считывания каждой литеры строки контроль передается от состояния к состоянию в соответствие с заданным множеством переходов. Если после считывания последней литеры строки автомат будет находится в одном из последних состояний, то строка принадлежит языку, принимаемому автоматом. Формально конечный автомат определяется 5-ю хар-ками:

1) Конечным множеством состояний K. 2) Конечным множеством входным алфавитом. 3)множеством переходом. 4)Начальным состоянием. 5)Множеством последних сотояний.

M=(K,VT,F,H,S)

Один из наиболее важных результатов теории конечных автоматов состоит в том, что класс языков, определяемых недетерминированными конечными автоматами, совпадает с классом языков, определяемых детерминированными конечными автоматами. Это означает, что для любого недетерминированного конечного автомата всегда можно построить детерминированный конечный автомат, определяющий тот же язык. Соответствие лексическому анализу заключается в том, что каждому языку 3-его типа соответствует детерминированный конечный автомат, распознающий строки этого языка. Исходя из этого, можно сказать, что написание лексического анализатора частично сводится к моделированию различных автоматов для распознавания конструкций языка, таких как идентификаторы, числа, ключевые слова и т.д. Лексический анализ вкл в себя просмотр компилируемой программы и распознавание лексем, составляющих предложение исходного текста. Точный перечень лексем, которые нужно распознать, зависит от ЯП и от грамматики, используемой для описания этого языка.

Лексический анализатор преобразовывает исх программу в последовтельность символов. При этом идентификаторы и константы производной длины заменяются символами фиксированной длины. Слова языка также заменяются какими-нибудь стандартными представлениями. Для повышения эффективности последних действий, каждая лексема обычно определяется кодом. Коды, создаваемые для слов языка, не должны зависеть от программы. В случае же идентификатора дополнительно необходимо конкретное имя распознаваемого идентификатора. Получение кодов-идентификаторов производится последовательно, начиная с начала по тексту проги. Кадый экземпляр определенного идентификатора на любом уровне заменяется одним и тем же кодом. Из этого следует необходимость создания таблицы идентификаторов, где будут храниться соответствия кодов и самих идентификаторов.

Аналогично таблиза необходима и для констант. Некоторые компиляторы проверяют длину констант и вычисляют их в процессе лексического анализа. Однако табл констант используется на более поздних стадиях компиляции, и поэтому ее обычно просто заполняют на этапе лексического анализа.

Сущ проблема с именами идентификаторов в том случае, если переменная с одинаковым именем присутствует в процедуре и в основной программе. В этом случае необходимо создавать столько строк в таблице идентификаторов, сколько раз определена данная переменная, кроме того нужно к таблице добавить поле для занесения информации о том, какой процедуре принадлежит идентификатор. При лексическом анализе базовым терминальным символом является буква, что вытекает их традиционного определения идентификаторов как последовательности букв и цифр, начинающихся с буквы. Еще более важным фактором является необходимое во всех языках наличие разделитилей или пробела между лексемами. Сам этот пробел и недопустимые буквы тяжелее всего распознать традиционными средствами грамматики. В дополнение к своей основной функции лексический анализатор обычно также выполняет чтение строк исходной программы и возможно печать листинга исходной программы. Многие языки имеют специфические особенности, которые должны учитываться при программировании лексического анализатора.

Компиляторы. Лексический анализ. Таблица сверток и диаграмма состояний.

Для того, чтобы при лексическом разборе быстрее находить правило с подходящей правой частью, фиксируют все возможные свертки в описании грамматики (это определяется только грамматикой и не зависит от вида анализируемой цепочки).

Это можно сделать в виде таблицы, строки которой помечены нетерминальными символами грамматики, столбцы - терминальными. Значение каждого элемента таблицы - это нетерминальный символ, к которому можно свернуть пару "нетерминал-терминал", которыми помечены соответствующие строка и столбец.

Например, для грамматики G = ({a, b, #}, {S, A, B, C}, P, S), такая таблица будет выглядеть следующим образом:

P: S  C#

C  Ab | Ba

A  a | Ca B  b | Cb

Знак "-" ставится в том случае, если для пары "терминал-нетерминал" свертки нет.

Чаще информацию о возможных свертках представляют в виде диаграммы состояний- неупорядоченного ориентированного помеченного графа, который строится следующим образом:

(1) строят вершины графа, помеченные нетерминалами грамматики (для каждого нетерминала - одну вершину), и еще одну вершину, помеченную символом, отличным от нетерминальных, - H. Эти вершины будем называть состояниями.H - начальное состояние.

(2) соединяем эти состояния дугами по следующим правилам:

a) для каждого правила грамматики вида W  t соединяем дугой состояния H и W (от H к W) и помечаем дугу символом t;

б) для каждого правила W  Vt соединяем дугой состояния V и W (от V к W) и помечаем дугу символом t.

Диаграмма состояний для грамматики G (см. пример выше):

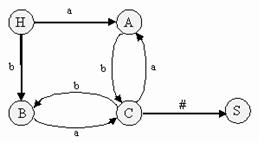
Тогда для диаграммы состояний применим следующий алгоритм разбора:

(1) объявляем текущим состояние H;

(2) затем многократно (до тех пор, пока не считаем признак конца цепочки) выполняем следующие шаги: считываем очередной символ исходной цепочки и переходим из текущего состояния в другое состояние по дуге, помеченной этим символом. Состояние, в которое мы при этом попадаем, становится текущим.

При работе этого алгоритма возможны следующие ситуации (аналогичные ситуациям, которые возникают при разборе непосредственно по регулярной грамматике):

(1) прочитана вся цепочка; на каждом шаге находилась единственная дуга, помеченная очередным символом анализируемой цепочки; в результате последнего перехода оказались в состоянии S. Это означает, что исходная цепочка принадлежит L(G).

(2) прочитана вся цепочка; на каждом шаге находилась единственная "нужная" дуга; в результате последнего шага оказались в состоянии, отличном от S. Это означает, что исходная цепочка не принадлежит L(G).

(3) на некотором шаге не нашлось дуги, выходящей из текущего состояния и помеченной очередным анализируемым символом. Это означает, что исходная цепочка не принадлежит L(G).

(4) на некотором шаге работы алгоритма оказалось, что есть несколько дуг, выходящих из текущего состояния, помеченных очередным анализируемым символом, но ведущих в разные состояния. Это говорит о недетерминированности разбора. Анализ этой ситуации будет приведен далее.