Расчёт схемы звезда – звезда без нулевого провода
Расчёт такой же, как и для схемы звезда - звезда с нулевым проводом. Только будет отсутствовать комплексная проводимость нулевого провода Y0, так как нет нулевого провода (рис. 21).
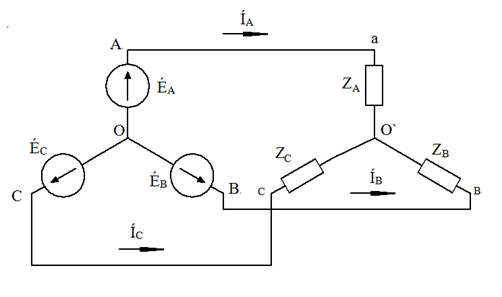
Рис. 21. Схема соединений звезда – звезда без нулевого провода
Для этой схемы
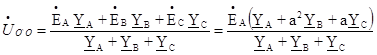(47)
Если нагрузка неравномерная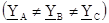 
, то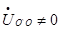 
и на фазах нагрузки будут разные напряжения:
ÚAO`=ÉА - ÚO`О, ÚВO`=ÉВ - ÚO`О, ÚСO`=ÉС - ÚO`О (48)
А токи в фазах нагрузки будут найдены:
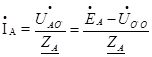; (49)
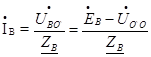; (50)
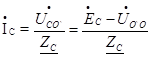; (51)
Линейные токи по отношению друг к другу могут находиться под любым углом, т. е. образуют несимметричную систему векторов. По первому закону Кирхгофа их сумма должна равняться нулю:
ÍA + ÍB + ÍC = 0. (52)
Если нагрузка равномерная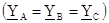 
, то:
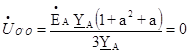(53)
так как 1 + а2 + а = 0
В этом случае линейные токи ÍA, ÍB, ÍC образуют симметричную систему векторов:
; 
; 
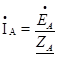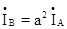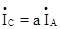; (54)
Естественно, что:
Í0 = ÍA + ÍB + ÍC = 0. (55)
Расчёт схемы, когда нагрузка соединена звездой и известны линейные напряжения (рис. 22)
Сюда подходят схемы соединений треугольник – звезда и звезда – звезда без нулевого провода.
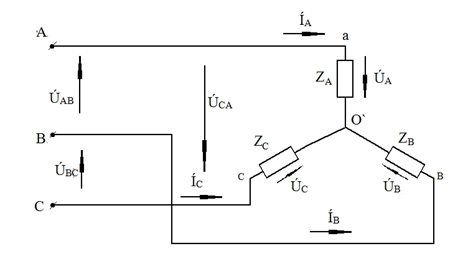
Рис. 22. Электрическая схема
По первому закону Кирхгофа можно записать:
ÍA + ÍB + ÍC = 0 (56)
Токи в фазах нагрузки можно записать через фазные напряжения нагрузок ÚA, ÚB, ÚC и комплексные проводимости нагрузок:
ÍA = ÚAYA; ÍВ = ÚВYВ; ÍС = ÚСYС; (57)
Подставим (57) в (56):
ÚAYA+ ÚВYВ+ ÚСYС = 0 (58)
Фазные напряжения ÚВ и ÚС могут быть выражены через ÚА и заданные линейные напряжения ÚАВ и ÚСА:
ÚАВ = ÚА - ÚВ; ÚВ = ÚА - ÚАВ; (59)
ÚСА = ÚС – ÚА; ÚС = ÚА + ÚАВ; (60)
Подставим (59) и (60) в (58):
ÚAYA+ (ÚА – ÚАВ)YВ+ (ÚА + ÚАВ)YС = 0.
Отсюда
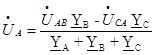(61)
Теперь фазные напряжения ÚА и ÚС выразим через ÚВ и заданные линейные напряжения ÚАВ и ÚВС:
ÚАВ = ÚА - ÚВ; ÚА = ÚВ + ÚАВ; (62)
ÚВС = ÚВ – ÚС; ÚС = ÚВ - ÚВС; (63)
Подставим (62) и (63) в (61):
(ÚВ + ÚАВ)YA+ ÚВYВ+ (ÚВ - ÚВС)YС = 0.
Отсюда
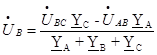(64)
Аналогично выразим ÚА и ÚВ выразим через ÚС и заданные линейные напряжения ÚСА и ÚВС:
ÚСА = ÚС – ÚА; ÚА = ÚС – ÚСА; (65)
ÚВС = ÚВ – ÚС; ÚВ = ÚС + ÚВС; (66)
Подставим (66) и (65) в (64):
(ÚС – ÚСА)YA+ (ÚС + ÚВС)YВ+ ÚСYС = 0.
Отсюда
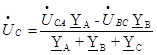(67)
Расчёт схемы, когда нагрузка соединена треугольником и известны линейные напряжения (рис. 23)
Сюда подходят схемы соединений треугольник – треугольник и звезда – треугольник.
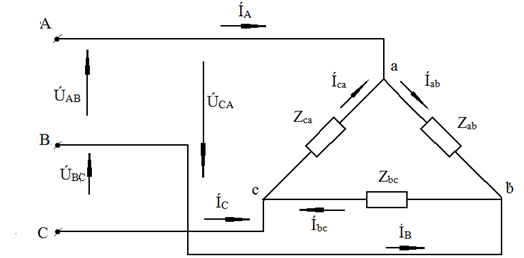
Рис. 23. Электрическая схема
Так как заданные линейные напряжения ÚAB, ÚBС, ÚСА напрямую подключаются к сопротивлениям нагрузки Zab, Zbc, Zca, то легко найти фазные токи нагрузок Íab, Íbc, Íca:
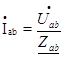
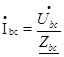
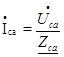(67)
Токи в линейных проводах определяются по первому закону Кирхгофа для узлов a, b, c:
ÍА + Ícа - Íab = 0; ÍА = Íаb – Íca; (68)
ÍВ + Íаb - Íbc = 0; ÍВ = Íbc – Íab; (69)
ÍС + Íbc – Íca = 0; ÍС = Íca – Íbc; (70)
Если на выводах несимметричной трёхфазной нагрузки, соединённой треугольником, заданы фазные напряжения источника ÚA, ÚB, ÚC, обмотки которого соединены в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений:
ÚAB = ÚA – ÚВ; ÚBС = ÚB – ÚС; ÚСА = ÚС – ÚС; (71)
Далее задача сводится к только что рассматриваемому случаю.
Дата добавления: 2015-07-30; просмотров: 5221;