Умови інваріантності

Розглянемо умови інваріантності розімкненої системи (рис.4.2.): Y(t) = 0.

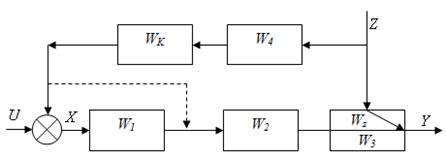
Рис. 4.2. Структурна схема розімкненої АСР

Вважаємо, що u = cоnst,а збурюючий сигнал Z діє на вихідну координату Y двома шляхами – по каналах Z →Y або Z →X→ Y . В операторній формі рівняння для вихідного сигналу має вигляд:

Y(s) = Z(s)[W_z(s)+W₁(s)W₂(s)W₃(s)W₄(s)₅W_к(s)]=0 /4.1/

За наявності збурення Z(s) ¹ 0 умова інваріантності /4.1/ виконується, якщо:

W_z(s)+ W₁(s)W₂(s)W₃(s)W₄(s)W_к(s)=0

З /4.1/ можна знайти передаточну функцію, яку повинен мати компенсатор, щоб виконувалась умова інваріантності:

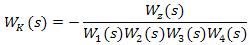/4.2/

Таким чином, щоб забезпечити інваріантність системи регулювання відносно якого-небудь збурення необхідно встановити динамічний компенсатор, передаточна функція якого дорівнює відношенню передаточної функції об’єкта по каналу збурення до передаточної функції еквівалентного об’єкту, взятого з протилежним знаком.

Якщо компенсуючий сигнал надходить на вхід виконавчого механізму, то умова інваріантності набере вигляду

W_z(s)+W₂(s)W₃(s)W₄(s)W_к(s)=0 /4.3/

Одержимо умови інваріантності для комбінованої АСР, якщо компенсуючий сигнал надходить на вхід регулятора (див. рис. 4.1, а). У цьому разі передаточна функція комбінованої системи регулювання по каналу Z →Y набере вигляду:

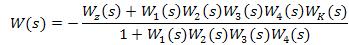/4.4/

Умова інваріантності комбінованої системи полягає в тому, що чисельник передаточної функції має дорівнювати нулю. Таким чином, у разі ввімкнення виходу компенсатора на вхід регулятора передаточна функція компенсатора, одержана з умови інваріантності, залежатиме від характеристик не лише об’єкта, а й регулятора.