В) MatLab

Среди ряда современных систем компьютерной математики особо выделяется математическая система MatLab.

Система MatLab предлагается разработчиками (MathWorks Inc) как лидирующий на рынке, в первую очередь на предприятиях военно-промышленного комплекса, в энергетике, в аэрокосмической отрасли и в автомобилестроении, язык программирования высокого уровня для технических вычислений, расширяемый большим количеством прикладных программ – расширений.

Популярности MatLab способствует ее матричная ориентация и мощное главное расширение Simulink. MatLab и Simulink поставляются в виде единого программного комплекса. Они предоставляют пользователю удобные и простые средства, в том числе визуального объектно-ориентированного программирования, для моделирования линейных и нелинейных динамических систем, а также множество других пакетов расширений системы. Некоторые из них являются наиболее доступными и эффективными инструментальными средствами для развития и применения новых направлений науки и техники, таких как нечеткая логика, нейронные сети, средства анализа и обработки сигналов и изображений, средства анализа, идентификации и моделирования систем и т.п.

Структура комплекса MatLab + Simulink помимо основы – MatLab и главного расширения Simulink содержит обширные группы пакетов расширений.

Этот инструментальный ящик Toolbox с числом пакетов расширения приближающимся к сотне, и группа пакетов расширения Blockset, расширяющая возможности системы визуально-ориентированного блочного моделирования динамических систем Simulink.

Одной из основных задач системы MatLab всегда было предоставление пользователям мощного языка программирования, ориентированного на технические и математические расчеты и способного превзойти возможности традиционных языков программирования, которые многие годы использовались для реализации численных методов. При этом особое внимание уделялось как повышению скорости вычислений, так и адаптивные системы к решению самых разнообразных задач пользователей.

3.2. Дискретно-детерминированные модели (F-схемы)

Использование F-схем позволяет формализовать процесс функционирования дискретно-детерминированных систем, для которых характерно наличие дискретных состояний и дискретный характер работы во времени [8].

Дискретно-детерминированные модели широко используются в качестве математического аппарата теории автоматов. Теория автоматов - это раздел технической кибернетики, в котором изучаются математические модели – автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени.

Автомат можно представить как некоторое устройство (чёрный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторое внутреннее состояние. Конечным автоматом называется автомат, у которого множества внутренних состояний, входных сигналов и выходных сигналов являются конечными множествами.

Абстрактный конечный автомат (англ. Finite Automata) математически задаётся F–схемой:

F = < X, Y, Z, φ, ψ, z₀ >, (3.30)

где X – конечное множество входных воздействий (входной алфавит);

Y – конечное множество выходных величин (выходной алфавит);

Z – конечное множество внутренних состояний (алфавит состояний);

z₀ – начальное состояние, z₀ Î Z;

φ(z, x) – функция переходов;

ψ(z, x) – функция выходов.

Автомат, задаваемый F–схемой, функционирует в дискретном времени t = nT, где T – период дискретности (такт, т.е. равный интервал времени); n = 0, 1, 2, 3… – номер такта.

На каждом такте дискретного времени F–автомат находится в определённом состоянии z(n) из множества Z состояний автомата, причём в начальный момент времени t = 0 он всегда находится в начальном состоянии z(0) = z₀. В момент времени t = nT, будучи в состоянии z(n), автомат способен воспринимать на входе сигнал x(n) Î X и выдавать на выходе сигнал y(n) = ψ[z(n), x(n)], переходя в состояние z(n+1) = φ[z(n), x(n)], z(n) Î Z, y(n) Î Y.

Таким образом, работа конечного автомата происходит по следующей схеме: в каждый n-й такт на вход автомата, находящегося в состоянии z(n), подаётся некоторый входной сигнал x(n), на который он реагирует переходом в (n+1)-м такте в новое состояние z(n+1) и выдачей некоторого выходного сигнала y(n).

Классификация конечных автоматов.F–автоматы разделяются по математическому описанию, по числу состояний и по характеру отсчёта дискретного времени.

По математическому описанию автоматы делятся на автоматы первого и второго рода.

F-автомат первого рода, называемый автоматом Мили, описывается следующими уравнениями:

, n = 0, 1, 2, 3… (3.31)

Для F-автомата второго рода уравнения имеют вид:

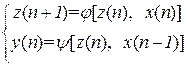, n = 0, 1, 2, 3… (3.32)

Автомат второго рода, для которого функция выходов не зависит от входной переменной x(n), называется автоматом Мура:

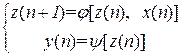, n = 0, 1, 2, 3… (3.33)

По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти обладают лишь одним состоянием. Автоматы без памяти ставят в соответствие каждому входному сигналу x(n) определённый выходной сигнал y(n), реализуя функцию вида y(n) = ψ[x(n)], n = 0, 1, 2, 3… .

По характеру отсчёта дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F–автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учётом считанного входного воздействия и в соответствии с уравнениями (3.31) – (3.33) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом времени между соседними синхронизирующими сигналами. Асинхронный F–автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины x(n), он может, как следует из (3.31) – (3.33), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое состояние, которое уже не может быть изменено данным входным сигналом [8].

Способы задания работы автоматов. Чтобы задать конечный F–автомат, требуется описать все элементы множества F = <X, Y, Z, φ, ψ, z₀ >, т.е. входной, выходной алфавиты и алфавит состояний, а также функции переходов и выходов. Причём среди множества состояний необходимо выделить состояние z₀, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы F–автоматов, но наиболее часто используются табличный, графический и матричный.

Табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояниям. При этом обычно первый слева столбец соответствует начальному состоянию z₀. На пересечении i-ой строки и k-го столбца таблицы переходов помещается соответствующее значение φ(z_k, x_i) функции переходов, а в таблице выходов – соответствующее значение ψ(z_k, x_i) функции выходов. Для F–автомата Мура обе таблицы совмещаются в отмеченную таблицу переходов, в которой над каждым состоянием z_k автомата, обозначающим столбец таблицы, ставится соответствующее этому состоянию значение ψ(z_k) выходного сигнала.

Описание работы F–автоматов Мили иллюстрируется табл.3.1, а пример табличного способа задания F–автомата Мили с тремя состояниями (z₀, z₁, z₂), двумя входными (x₁, x₂) и двумя выходными (y₁, y₂) сигналами приведён в табл.3.2.