Транспортне запізнення

Рис. 2.24. Транспортне Рис. 2.25. Довга лінія як ланка з запізненням.
запізнення
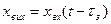
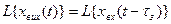
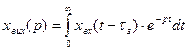
Введемо змінну 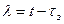 .
.
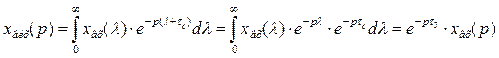
АФЧХ ланки з запізненням зображена на рис. 2.26.

Рис. 2.26.
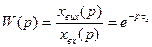
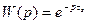
Ланки, які мають чисте запізнення зустрічаються дуже рідко. Частіше вони зустрічаються в поєднанні з ланками, що вносять відставання чи випередження.
АФЧХ ланки з запізненням + (відставання чи випередження) на високих частотах перетворюється в спіраль, що охоплює початок координат.
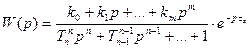
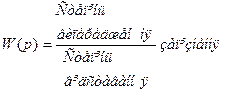
1.
 |
Ланка з запізненням + ланка з відставанням


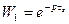 ;
; 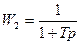
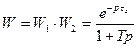
2.  Ланка з запізненням + інтегруюча ланка
Ланка з запізненням + інтегруюча ланка

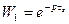 ;
; 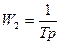
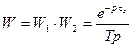
3.  Ланка з запізненням + диференціююча ланка
Ланка з запізненням + диференціююча ланка
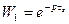
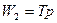


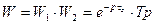
2.16. Поняття стійкості. Стійкість лінійних динамічних систем
Стійкість – здатність системи повертатись в стан рівноваги після припинення дії вимушуючих сил (вхідна дія, збурення).
Стійкість нас цікавить тому, що нестійкі системи – непрацездатні. Невеличкі збурення виводять їх з планової траєкторії, до якої вони ніколи не зможуть повернутися.
Стійкість – внутрішня властивість системи, яка не залежить від величини вхідної дії чи від величини збурення.
 Для великих систем ця характеристика вироджується в надійність чи живучість.
Для великих систем ця характеристика вироджується в надійність чи живучість.
1. Стійка система – оцінка стійкості не залежить від А1, А2 і т.д.
2. Система нестійка
3.
 |
r ® ¥ - стан байдужої рівноваги.
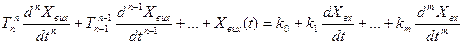 – рівняння руху системи
– рівняння руху системи
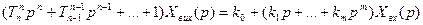
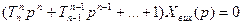 - характеристичне рівняння
- характеристичне рівняння
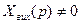
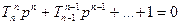 - для оцінки стійкості знаменник передатної функції необхідно прирівняти до нуля.
- для оцінки стійкості знаменник передатної функції необхідно прирівняти до нуля.
Загальний розв’язок характеристичного рівняння має вигляд:
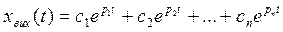 , де
, де
с1,с2,с3,...,сn – постійні інтергування
p1,p2,p3,...,pn – корені характеристичного рівняння.
Корені характеристичного рівняння можуть мати такі випадки:
1. Всі дійсні додатні – система нестійка, процес розходиться
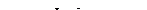 Якщо хоча б один корінь додатній - система нестійка.
Якщо хоча б один корінь додатній - система нестійка.
2. Всі дійсні від’ємні - система стійка
Якщо всі корені від’ємні - система стійка.
3. Комплексні корені
Для стійкої системи дійсні частини комплексних коренів повинні бути від’ємними (лежати в лівій площині) (рис. 2.27).
Рис. 2.27.
Дата добавления: 2015-07-24; просмотров: 1054;
