ОСОБЕННОСТИ ТВОРЧЕСКОГО МЫШЛЕНИЯ
Прежде чем излагать взгляды психологов на проблему творческого мышления, рассмотрим некоторые факты, которые помогут лучше понять сформулированные дальше положения, касаю-
^Блейлер Э. Аутастическое мышление // Хрестоматия по общей психологии: Психология мышления. — М., 1981. — С. 122.
щиеся данного вида мышления. С самого начала отметим, что творческое мышление не обязательно связано только с одним из обсуждавшихся ранее видов мышления, скажем, словесно-логическим; оно вполне может быть и практическим, и образным.
РАрнхейм отмечает, что видеть свойства какого-либо предмета — значит воспринимать его как пример воплощения определенного общего понятия, что всякое восприятие состоит в выделении ранее абстрагированных черт. «Следовательно, абстрактное содержится не только в мышлении, но и в других познавательных процессах»1.
Ярким примером необходимости наглядно-образных представлений для более глубокого понимания абстрактных вещей и понятий может служить следующий пример. Оказывается, что такие различные геометрические понятия, как точка, прямая, треугольник, трапеция, окружность, эллипс, парабола, которые благодаря подкупающей простоте и законченности строения считались абстракциями, не зависящими от реальности, на самом деле связаны с ней и с конкретно-образными представлениями. Рисунок 52 наглядно демонстрирует, что все эти абстракции можно «увидеть» на различных сечениях плоскостью обыкновенного конуса. Точка получается, если плоскость проходит через вершину конуса (52.1); треугольник образуется при пересечении плоскостью конуса по его оси (52.2); отрезок прямой линии можно получить, если плоскость проходит как касательная к боковой поверхности конуса (52.3); трапеция образуется в случае, если от треугольника, образуемого сечением 52.2, отделяется верхняя часть при помощи плоскости, параллельной основанию (52.4); круг можно получить, сделав поперечное сечение конуса плоскостью, параллельной основанию (52.5), эллипс образуется таким же сечением, но проведенным под наклоном (52.6); парабола вырисовывается в случае, если секущая плоскость проходит параллельно оси конуса, но не через ее саму (52.7). Таким образом, меняя расположение и взаимную ориентацию конуса и секущей плоскости, можно не только получить ряд фигур, выражающих абстрактные понятия, но и незаметно, в наглядно-действенном плане переходить от одного абстрактного понятия к другому.
По этому поводу Р.Арнхейм пишет, что элементы мышления в восприятии и восприятия в мышлении взаимно дополняют друг друга. «Они превращают человеческое познание в еди-
^Арнхейм Р. Визуальное мышление // Хрестоматия по общей психологии: Психология мышления. — М., 1981. — С. 98.
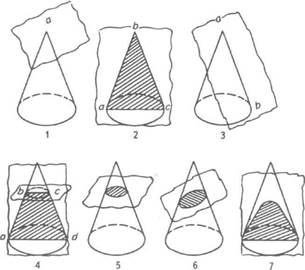
Рис. 52. Примеры наглядного представления основных абстрактных геометрических понятий в виде сечений конуса плоскостью
ный процесс, который ведет неразрывно от элементарного приобретения сенсорной информации к самым обобщенным теоретическим идеям»1.
Психологами было затрачено много усилий и времени на выяснение того, как человек решает новые, необычные, творческие задачи. Однако до сих пор ясного ответа на вопрос о психологической природе творчества нет. Наука располагает только некоторыми данными, позволяющими частично описать процесс решения человеком такого рода^ задач, охарактеризовать условия, способствующие и препятствующие нахождению правильного решения. Прежде чем их рассматривать, обратимся к некоторым простейшим примерам задач творческого типа для того, чтобы выяснить их особенности (рис. 53).
Дата добавления: 2015-07-24; просмотров: 673;
