Электрических цепях постоянного тока

При анализе электрических цепей широко используются закон Ома и законы Кирхгофа. Задача анализа электрической цепи состоит в том, что схема цепи и параметры ее элементов известны. Требуется определить токи в ветвях схемы, напряжения на элементах, мощности и так далее.

Различают формулировки закона Ома для участка цепи с пассивным элементом, для участка цепи с источником ЭДС и для замкнутой цепи. Рассмотрим эти формулировки поочередно.

Закон Ома для участка цепи с пассивным элементом. Схема участка цепи постоянного тока с пассивным элементом приведена на рис. 2. Согласно закону Ома ток I на участке ab цепи c пассивным элементом прямо пропорционален напряжению U_ab и обратно пропорционален сопротивлению R

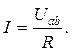(1)

Формулу закона Ома можно выразить и через проводимость g=1/R:

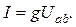
Закон Ома для участка цепи с источником ЭДС. Схема участка цепи постоянного тока с источниками ЭДС приведена на рис. 5. Участок состоит из последовательного соединения сопротивлений и источников ЭДС и является частью сложной схемы.

Рис. 5. Участок электрической цепи с пассивными элементами и

источниками ЭДС

Примем положительное направление тока от a к b и выразим потенциалы всех точек схемы через потенциал одной точки, например, точки a. При переходе через сопротивление R₁ потенциал убывает на величину падения напряжения R₁I, т.е.

φ₁ = φ_a – R₁I.

При переходе через источник ЭДС E₁ потенциал возрастает на величину E₁:

φ₂ = φ₁ + E₁= φ_a – R₁I + E₁.

При переходе через сопротивление R₂ потенциал снова убывает на величину падения напряжения R₂I:

φ₃ = φ₂ – R₂I = φ_a – R₁I + E₁– R₂I.

При переходе через источник ЭДС E₂ потенциал убывает на величину E₂:

φ₄ = φ₃ – E₂= φ_a – R₁I + E₁– R₂I – E₂.

И, наконец, при переходе через сопротивление R₃ потенциал убывает на величину падения напряжения R₃I:

φ_b = φ₄ – R₃I = φ_a – R₁I + E₁– R₂I – E₂ – R₃I.

Полученные формулы выражают закон распределения потенциала вдоль рассматриваемого участка электрической цепи (рис. 5).

Решая последнее уравнение относительно тока, находим выражением закона Ома для рассматриваемой схемы:

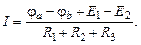
Обобщая эту формулу, получаем выражение закона Ома для участка цепи с источниками ЭДС в общем случае:

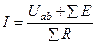, (2)

где U_ab = φ_a – φ_b – напряжение на участке ab; 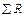– арифметическая сумма сопротивлений на участке ab; 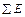– алгебраическая сумма ЭДС на участке ab. Причем E берется со знаком «плюс», если направление действия ЭДС и выбранное положительное направление тока совпадают. В противном случае перед E берется знак «минус».

Используя полученные выше формулы, выражающие закон распределения потенциала вдоль рассматриваемого участка электрической цепи, можно построить график изменения потенциала в функции сопротивления, который носит название потенциальной диаграммы (рис. 6).

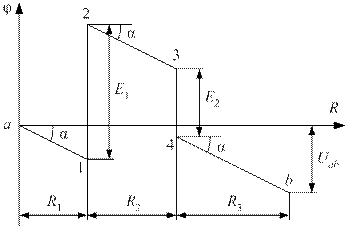
Рис. 6. Потенциальная диаграмма участка электрической цепи

При построении потенциальной диаграммы потенциал одной из точек схемы обычно принимается равным нулю. На рис. 6 φ_a = 0. По оси абсцисс откладываются сопротивления, по оси ординат – потенциалы точек схемы. При построении потенциальной диаграммы, представленной на рис. 6, обход участка электрической цепи принят от точки a к точке b – по току. Поэтому на участках электрической цепи, содержащих сопротивления R₁, R₂, R₃, потенциал убывает по линейному закону. На рис. 6 эти участки представлены отрезками прямых между точками a и 1, 2 и 3, 4 и b. Наклон отрезков прямых к оси абсцисс одинаков и пропорционален току I участка цепи:

,

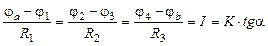где K – масштабный коэффициент, равный отношению масштаба потенциалов к масштабу сопротивлений и имеющий размерность тока; α – угол наклона отрезков прямых к оси абсцисс на рис. 6.

При переходе через источник ЭДС потенциал меняется скачкообразно на величину ЭДС, поскольку в рассматриваемой схеме источники ЭДС идеальные и их внутренние сопротивления равны нулю. Причем при переходе через E₁ потенциал скачкообразно возрастает, при переходе через E₂ – скачкообразно убывает, что обусловлено направлением действия соответствующего источника ЭДС.

Закон Ома для замкнутой цепи. Простейшая схема замкнутой цепи постоянного тока приведена на рис. 1. Ток I в замкнутой цепи пропорционален ЭДС Е и обратно пропорционален суммарному сопротивлению всей цепи. Если сопротивлением соединительных проводов можно пренебречь, то для цепи рис. 1

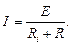(3)

Формулы (1), (2), (3) являются выражениями закона Ома соответственно для участка цепи с пассивным элементом, для участка цепи с источником ЭДС и для замкнутой цепи. Используя эти выражения необходимо иметь в виду, что при малой длине соединительных проводов их сопротивлением, как правило, пренебрегают. При достаточной протяженности соединительных проводов их сопротивление R_л становится соизмеримым с внутренним сопротивлением источника R_i и сопротивлением приемника R. В этом случае его необходимо учитывать в суммарном сопротивлении цепи.

Сопротивление металлического проводника линии передачи можно определить по формуле

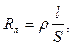
где r - удельное сопротивление проводника [Ом∙мм²/м];

l – длина проводника [м];

S – площадь сечения проводника [мм²].

Сопротивление металлического проводника зависит от температуры. Эта зависимость выражается формулой

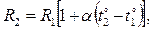
где R₁, R₂ – сопротивления для двух разных температур t₁° и t₂°;

a – коэффициент, зависящий от материала [1/град].

Температура является одной из причин нелинейности сопротивления. Но при малых изменениях температур сопротивления металлических проводников можно считать линейными.

Законы Кирхгофа. Законами Кирхгофа в электротехнике называют два правила, которые используются для описания процессов в разветвленных электрических цепях. Прежде, чем сформулировать законы Кирхгофа, целесообразно определить такие понятия разветвленной цепи, как узел, ветвь и контур.

Узел – это точка схемы, в которой сходятся не менее трех ветвей. Пример узла электрической цепи приведен на рис. 7.

Рис. 7. Пример узла электрической цепи

Ветвь– это участок электрической цепи между двумя узлами, состоящий из последовательно соединенных источников и приемников электрической энергии. В соответствии с законом непрерывности электрического тока, через все последовательно включенные элементы одной ветви протекает один и тот же ток. На рис. 8 приведена схема участка электрической цепи, на которой изображены три ветви, соответственно ab, bc и ca.

Контуромназывается последовательный замкнутый обход по нескольким ветвям схемы. Пример контура электрической цепи, образованного тремя ветвями, приведен на рис. 8.

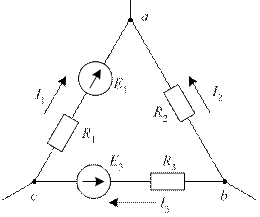
Рис. 8. Пример контура электрической цепи

Законы Кирхгофа можно сформулировать следующим образом.

Первый закон: Алгебраическая сумма токов в узле в любой момент времени равна нулю.

Для цепи постоянного тока первый закон Кирхгофа выражается формулой

где k – текущий номер ветви, входящей в узел;

p – число ветвей, входящих в узел.

Слова «алгебраическая сумма» предполагают, что все токи, выходящие из узла, берутся с одним знаком, например, с плюсом. Все токи, входящие в узел, берутся с другим знаком, например, с минусом. Для узла a на рис. 7 первый закон Кирхгофа позволяет составить следующее уравнение:

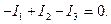
Второй закон: В любом замкнутом контуре в любой момент времени алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, действующих в контуре.

Для цепи постоянного тока это можно записать как

где l– текущий номер падения напряжения;

q – число падений напряжений в контуре (число пассивных элементов в контуре);

j – текущий номер источника ЭДС;

d– число источников ЭДС в контуре.

При составлении уравнения по второму закону Кирхгофа необходимо вначале задаться направлением обхода контура. Если падения напряжений и ЭДС совпадают по направлению с напряжением обхода контура, то в уравнении второго закона Кирхгофа они берутся со знаком плюс. В противном случае они берутся со знаком минус. Изменение направления обхода контура равносильно умножению уравнения второго закона Кирхгофа на минус единицу.

Направление обхода контура для схемы рис. 8 выбрано по часовой стрелке. В соответствии со вторым законом Кирхгофа для этого контура справедливо следующее уравнение

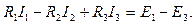
Падения напряжений на сопротивлениях R₁ и R₃ совпадают с направлением обхода контура. В уравнении они взяты со знаком плюс. Падение напряжения на сопротивлении R₂ противоположно направлению обхода контура. В уравнении оно взято со знаком минус. Направление ЭДС Е₁ совпадает с направлением обхода контура, а Е₃ не совпадает. Поэтому в правой части уравнения взята разность Е₁ – Е₃.