Следствия из теплового закона Нернста
Некоторые положения, которые мы рассмотрим здесь как следствия из теплового закона Нернста, послужили основанием для его формулировки.
Следствие 1.
При абсолютном нуле температур энтропия системы, в которой протекает химическая реакция, не изменяется.
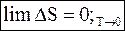 (7 - 38)
(7 - 38)
Следствие 2.
При абсолютном нуле температур теплоемкость системы не изменяется.
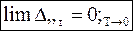 (7 - 38а)
(7 - 38а)
Следствие 3.
Для конденсированных систем постоянные интегрирования в уравнениях Гиббса - Гельмгольца и изобары химической реакции равны 0.
Это следствие основано на применении интегральной формы уравнения Гиббса - Гельмгольца
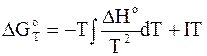 .
.
В соответствии с равенством (7 - 37) производная DG по температуре должна быть равна 0. Это возможно лишь при условии что,
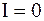 . (7 - 39)
. (7 - 39)
Последнее следствие открыло возможности расчета константы равновесия по термохимическим данным. Схему таких расчетов можно представить следующим образом.
Интегральная форма уравнения Гиббса - Гельмгольца с учетом выражения (7 - 39) принимает вид:
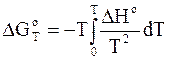 . (7 - 40)
. (7 - 40)
Интегральная форма уравнения Кирхгофа может быть представлена для данного случая так:
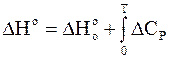 . (7 - 41)
. (7 - 41)
Подстановка вместо DН правой части уравнения (7 ‑ 41) в уравнение (7 - 40) дает
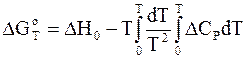 . (7 - 42)
. (7 - 42)
Если температурная зависимость теплоемкостей установлена, а тепловой эффект реакции может быть рассчитан по следствиям из закона Гесса, то уравнение (7 - 42) позволяет найти изменение энергии Гиббса, в том числе и стандартную величину. Далее по уравнениям (7 - 31) - (7 - 33) рассчитываются соответствующие константы равновесия.
Для систем, содержащих газы, тепловой закон в прямой форме не применим.
Нернст предложил для расчета констант равновесия в газовых и гетерогенных системах воспользоваться циклическим процессом, который включал бы в себя переход из конденсированного состояния в газовое и соответствующую химическую реакцию. Интегрирование уравнения Клапейрона - Клаузиуса для процессов испарения и возгонки приводит к появлению констант, называемых химическими постояннымиjk. Нернст показал, что алгебраическая сумма химических постоянных равна постоянной интегрирования уравнения изобары для газовых систем, т.е. I= Snj`jj`-Sniji ºDj.
Постулат Планка как формулировка третьего начала
М. Планк предложил еще одну формулировку третьего постулата, названную постулатом Планка:
При абсолютном нуле температур энтропия совершенных (идеальных) кристаллов чистого вещества равна 0.
Математическая запись постулата Планка такова:
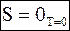 . (7 - 43)
. (7 - 43)
Постулат Планка выполняется для чистых твердых веществ, у которых кристаллы не имеют ни дефектов строения, ни дефектов включения, а термодинамическая активность равна 1.
Ранее указывалось, что существуют состояния чистых веществ, у которых термодинамическая активность не может считаться равной 1. К их числу относится стеклообразное состояние. Отсутствие кристаллической структуры, в которую возможен потенциальный переход стеклообразной структуры, означает неприменимость для него постулата Планка.
Таким образом, вещества со стеклообразной структурой при абсолютном нуле температур могут иметь энтропию, отличную от нуля.
Постулат Планка позволил решить проблему нахождения абсолютного значения энтропии для чистых веществ, имеющих при абсолютном нуле температур кристаллическую структуру.
Существенным дополнением к постулату Планка является равенство нулю теплоемкости при абсолютном нуле температур. Значения функции СР = СР( Т) , начиная с абсолютного нуля температур, для многих веществ известны.
Абсолютная энтропия чистого кристаллического вещества, не претерпевающего аллотропических переходов при нагревании от абсолютного нуля температур до данной температуры, вычисляется по уравнению (4 - 12):
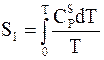 .
.
Если в дальнейшем происходит изменение кристаллической структуры (аллотропический переход) или фазовый переход при температуре Т1, то этот процесс сопровождается тепловым эффектом DН1. Изменение на этой стадии энтропии окажется равным
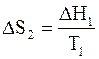 .
.
Последующее повышение температуры до нового фазового перехода приводит к
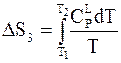 .
.
Новый фазовый переход при температуре Т2 вновь увеличит энтропию на DS3
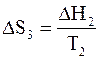 .
.
Дальнейшее повышение температуры вновь приводит к увеличению энтропии
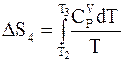 .
.
Если при температуре Т3 происходит следующий фазовый переход, то вновь изменение энтропии окажется равным отношению изменения энтальпии к температуре фазового перехода и т.д.
Абсолютное значение энтропии представляет собой сумму изменений энтропии на всех стадиях процесса вплоть до данной температуры
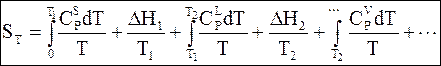 (7 - 44)
(7 - 44)
По уравнению (7 - 44) рассчитывается абсолютная величина энтропии для внесения в справочники химических величин. По принятым условиям IUPAC эти данные относятся к стандартной температуре и стандартному давлению. Стандартная энтропия обозначается 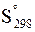 .
.
Дата добавления: 2015-07-24; просмотров: 1387;
