Скелет конечностей человека

Скелет каждой конечности разделяется на пояс и свободный отдел (см. рис. 2.14). Пояс расположен в пределах туловища, яв­ляется для конечностей опорой и соединяет их свободный отдел со скелетом туловища.

Пояс верхней конечности состоит из двух отдельных парных костей — ключицы и лопатки.

Свободный отдел состоит из трех частей: проксимальный (плечо), средний (предплечье) и дистальный (кисть).

Пояс нижней конечности образован с каждой стороны одной тазовой костью. Тазовая кость сочленяется с крестцом и с ближай­шей костью свободного отдела конечности (бедренной костью).

Свободный отдел состоит из трех частей: проксимальной (бед­ро), средней (голень) и дистальной (стопа).

Кости человеческого тела соединяются между собой посредст­вом плотной волокнистой соединительной ткани, эластической ткани и хряща.

Все соединения костей можно разделить на две группы: в пер­вой связующая ткань представляет сплошную прослойку между костями; это непрерывные соединения — синартрозы, большей частью малоподвижные или неподвижные. Подвижность их оп­ределяется растяжимостью той ткани, которая соединяет кости. Вторую группу составляют прерывные соединения более или менее подвижные, иначе сочленения, или суставы; здесь в ткани,

соединяющей кости, имеется полость, непрерывность связи меж­ду костями нарушается.

Некоторые кости, например, позвонки, связаны между собой различными видами соединений, среди которых имеются суставы, синхондрозы, синдесмозы.

Следует отметить, что суставы верхней конечности отличают­ся большей свободой и разнообразием движений, суставы нижней конечности также весьма подвижны при меньших степенях свобо­ды в некоторых из них (например, в тазобедренном по сравнению с плечевым, или в голеностопном по сравнению с лучезапястным и т. д.).

Нижние конечности человека служат исключительно для опо­ры и передвижения тела, а верхние, свободные от этой работы, раз­вились в орган трудовой деятельности.

Кроме скелета, система органов движения включает муску­латуру (см. рис. 13.2). Мышца соединяется с костью сухожилием посредством врастания коллагеновых волокон в надкостницу или надхрящницу, либо непосредственно в кость или хрящ. Сухожи­лия обеспечивают крепление мышц к костям, а также передачу мы­шечных усилий.

Прочность сухожилия при растяжении достигает от 44 до 67 МПа, хотя для дельтовидного сухожилия было получено значение раз­рушающего напряжения порядка 0,6 МПа.

Поперечнополосатые мышцы теснейшим образом (анатомичес­ки и физиологически) связаны со скелетом, образуя вместе с ним систему органов опоры и движения.

Общее число скелетных мышц в теле человека — более 600. Масса их составляет у женщин до 28—35% от массы тела, у муж­чин — до 40—45%, у спортсменов — 55—65%. Приблизительно 50% общей массы скелетных мышц приходится на нижние конеч­ности, 30% — на верхние конечности и 20% — на мышцы головы и туловища.

Скелетные мускулы, которые начинаются от костей (иногда от фасций и их производных), к костям и прикрепляются.

Важным в механике является вспомогательный аппарат мышц, включающий фасции, синовиальные сумки, влагалища сухожилий, блоки мышц, сесамовидные кости.

Фасции — фиброзные оболочки, покрывающие мышцы и отдель­ные группы мышц. Фасции выполняют опорную функцию, крепятся к кости образуя фасциальные футляры.

Синовиальные сумки — тонкостенные изолированные мешоч­ки, не связанные с полостью сустава и содержащие синовиальную жидкость.

Влагалища сухожилий — защитные приспособления сухожи­лий мышц в местах их наиболее тесного прилегания к кости (в об­ласти кисти и стопы). Они уменьшают трение, облегчая работу мышц.

Обычно мышцы действуют на кости, соединенные между сус­тавами, так что получается тот или иной род рычага. Особенно ясно выражено это на конечностях: здесь длинные кости образуют сис­тему легких и прочных рычагов, и в то же время представляют об­ширную поверхность, где прикрепляется высокодифференцирован-ная мускулатура.

Примером рычага первого рода может служить работа мышц при удержании головы (рис. 17.40) или тела в тазобедренном сус­таве. При удержании груза в руке, согнутой в локтевом суставе, образуется рычаг второго рода (рис. 17.41).

В механике подвижное соединение двух звеньев, находящихся в непосредственном соприкосновении, называют кинематической парой. Кинематические пары могут быть вращательными и посту­пательными. В зависимости от числа ограничений, накладываемых на движение, звенья могут совершать от одного до пяти движе­ний. В человеческом организме число независимых движений кос­тей в суставах может составлять от одного до трех. На рис. 17.42 показана кинематическая схема ОДА человека, на которой кости представлены в виде звеньев кинематической цепи, а суставы — кинематических пар.

При исследовании движений человека широко применяют кине­матические модели на основе уравнений движения системы твер­дых тел, которые соответствуют отдельным сегментам тела по гео­метрическим и масс-инерционным характеристикам; элементы модели соединяются вращательными шарнирами, диапазоны по­воротов которых соответствуют амплитудам угловых движений суставов; механические связи модели с окружающей средой час­то заменяют действием сил реакции, что позволяет сохранять структуру модели при различных движениях.

Важной особенностью таких биомеханических моделей явля­ется их ветвящаяся структура типа «дерево». Отсчет координат может начинаться от различных элементов в зависимости от того, какие из них находятся в контакте с опорой.

В зависимости от целей исследования можно условно разделить модели такого типа на две группы: кинематические и динамиче­ские (И.Ф. Образцов и др., 1983). Кинематическими называют модели, предназначенные для описания движений тела человека и дающие зависимости угловых и линейных перемещений (скоро­стей, ускорений) отдельных его точек в функции времени. Дина­мические модели позволяют оценивать распределение сил, напря­жений и деформаций в различных сегментах, структурах и тканях тела человека, в частности, для модельной оценки переносимости различных динамических воздействий.

Кинематика опорно-двигательного аппарата (ОДА)

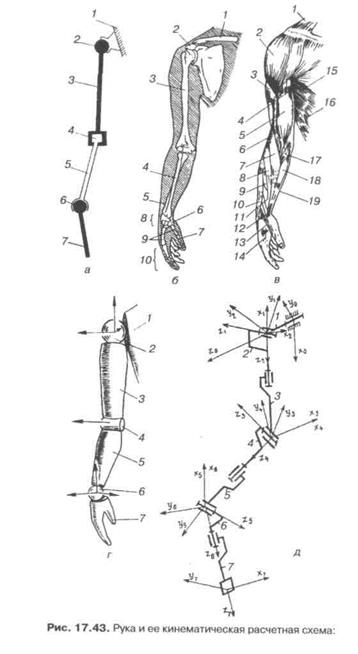
Рассмотрим кинематику руки человека (рис. 17,43). С точки зре­ния биомеханики, верхняя конечность может быть смоделирована многозвенным пространстввенным механизмом (рис. 17.43, д). Эта

система имеет семь степеней свободы. Плечевой сустав является шаровидным, т. е. имеет три степени свободы. На рис. 17.43, г он представлен эквивалентной схемой одноосных шарниров, оси вра­щения которых пересекаются в одной точке, а звенья 1, 2 имеют нулевую длину. Значит, положение седьмой системы координат в абсолютной, нулевой системе координат определяет формула:

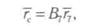
где — f_e — радиус-вектор точки С в абсолютной системе коорди­натных осей; г₇ — радиус-вектор точки С в седьмой системе коор­динат.

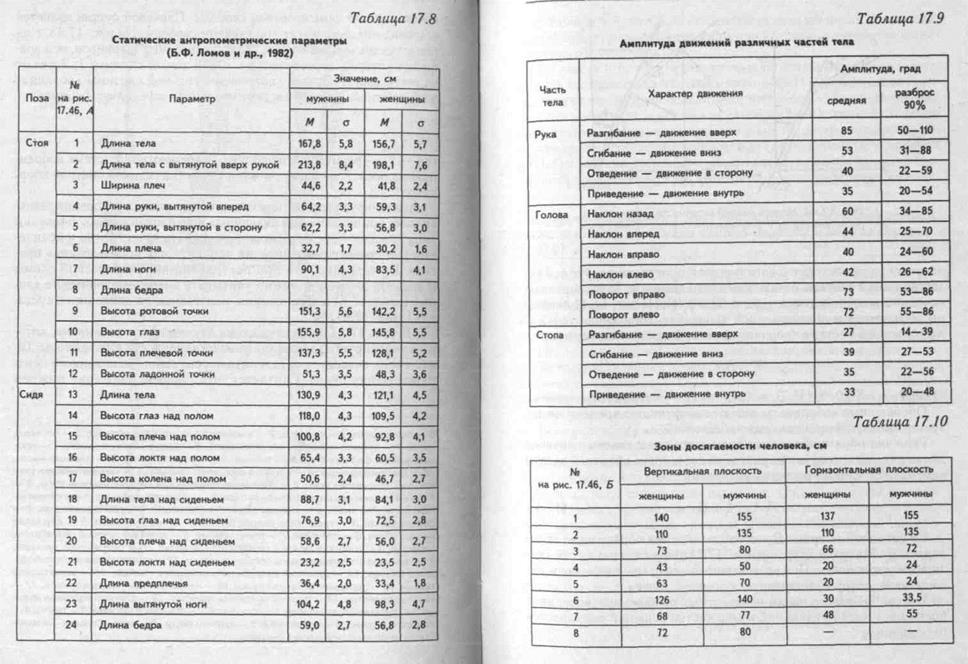
Анализируя угловые перемещения, скорости и ускорения звень­ев руки при исполнении различных целенаправленных движений типа «возьми—поставь» можно оценивать качественно и количе­ственно процесс реабилитации пациента или использование про­теза. Естественно, что при построении кинематической схемы и анализа движений нужно учитывать антропометрические дан­ные (табл. 17.8) и ограничения, налагаемые на движения в суста­вах (табл. 17.9).

На рис. 17.44 приведена схема двухзвенного механизма, кото­рым моделируется движение нижней конечности в фазе опоры. Та­кая схема позволяет определить перемещение мгновенного цент­ра вращения бедра. Считается, что плоское движение нижней

б — скелет руки: 1 — ключица, 2 — клювовидный отросток лопатки, 3 — плечевая кость, 4 — лучевая кость, 5 — локтевая кость, 6 — трапециевидная кость, 7 — про­ксимальная фаланга большого пальца, 8 — кости запястья, 9 — пястные кости, 10 — фаланги пальцев, д — система координат звеньев; а — кинематическая схе­ма: 1 — «плечевой» пояс, 2 — плечевая сферическая кинематическая пара, 3 — плечо, 4 — локтевая цилиндрическая пара, 5 — предплечье, 6— кистевая сфериче­ская пара, 7 — кисть, в — мышцы верхней конечности: 1 — трапециевидная, 2 — дельтовидная, 3 — трехглавая мышца плеча, 4 — клювоплечевая, 5 — двуглавая мышца плеча, 6 — плечевая, 7 — плечелучевая, 8 — длинный лучевой разгибатель запястья, 9 — короткий лучевой разгибатель запястья, 10 — разгибатель пальцев, ' 1 — длинная отводящая мышца большого пальца, 12 — короткий разгибатель боль­шого пальца, 13 — длинный разгибатель большого пальца, 14 — межкостная мышца, 15 — передняя зубчатая мышца, 16 — наружная косая мышца живота, 17 — круглый пронатор, 18 — лучевой сгибатель запястья, 19 — длинная ладонная мыш­ца, г — динамическая модель: 7 — туловище, 2 — плечевой шарнир, 3 — плечо, 4 — локтевой шарнир, 5 — предплечье, 6 — шарнир кисти, 7— кисть. Стрелки — компо­ненты мышечных моментов в суставах

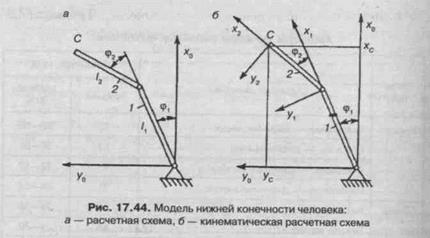
конечности происходит в сагиттальной плоскости вокруг оси го­леностопного сустава, остающейся неподвижной. За обобщенные координаты принимаются углы ф,(/) и <р₂(0. На рис. 17.44 показа­ны абсолютная и локальные оси координат. Положение точки С в абсолютной системе координатных осей находят по формуле:

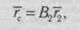
Здесь г₂ = (0,0, 0, 1 )^т; В₂ = Л Д, где Л. — матрица положения.

Обобщенные координаты задают как функцию времени по ре­зультатам экспериментальных наблюдений.

Решение обратной задачи кинематики представляют интерес для медицины и спорта. Формальная постановка обратной задачи кинематики требует решения уравнения:

По заданной матрице В. необходимо найти обобщенные коор­динаты g.. Матричное уравнение (17.1) эквивалентно шести ска­лярным уравнениям. При этом важно число степеней свободы ме­ханизма со, который модулирует органы человека.

1. Если со > 6, то число неизвестных обобщенных координат превышает число уравнений и множество решений оказывается бесконечным.

2. Если со < 6, то число неизвестных меньше числа уравнений. Задача будет иметь решение лишь при некоторых специальных по­ложениях механизма.

3. Если со = 6, то, приравняв наддиагональные элементы мат­риц 4-4, стоящих слева и справа в уравнении (17.1), можно получить систему из шести трансцендентных уравнений относительно обоб­щенных координат g Если это решение дает законы изменения обобщенных координат во времени g.(t), то, дифференцируя g.(t), можно найти обобщенные скорости g.(t) и обобщенные ускорения g.(t). Однако при этом погрешности расчета велики из-за необхо­димости использования методов численного дифференцирования.

Антропометрические и масс-инерционные характеристики тела человека. Динамика опорно-двигательного аппарата (ОДА)

Тело человека представляет собой сложную биомеханическую систему, которая в повседневной жизни может испытывать значительные ускорения, а в спорте высших достижений особен­но. При этом возникают усилия, приводящие к нарушению коор­динации движений, травмам и прочим изменениям в тканях ОДА.

Исследования движений человека (спортсмена) аналитически­ми методами механики проводятся с помощью моделей различной сложности, заменяющих ОДА и воспроизводящих действительную картину движений со степенью точности, достаточной для постав­ленных в процессе исследований задач.

Все сочленения звеньев тела можно моделировать геометриче­ски идеальными вращательными шарнирами.

Чтобы воспроизвести движения тела человека, в моделях из мак­симально возможных шести измеряемых движений для каждого твер­дого звена, когда оно не присоединено к соседним звеньям (трех по­ступательных и трех вращательных относительно трех координатных осей, фиксированных на соседнем звене), при наложении кинема­тических связей исключаются все поступательные и остаются лишь вращательные движения, причем нередко допускаются только неко­торые вращательные движения из трех возможных. Все оставшиеся вращательные движения составляют степени свободы звеньев.

Формула для определения числа степеней свободы ОДА в целом:

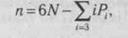
где и — число степеней свободы; N — число подвижных звеньев в модели тела; / — число ограничений степеней свободы в соеди­нениях-суставах; Р. — число соединений с ( ограничениями. При этом ЕР. = N — /.

Общее число степеней свободы тела человека составляет око­ло 6 • 144 — 5 • 81 — 4 • 33 — 3 • 29 = 240 (A. Morecki et al., 1969), но с полной достоверностью точное число неизвестно в связи с при­ближенным характером модели.

По кинематической схеме модели (см. рис. 17.43), подобно уп­рощенному скелету руки (см. рис. 17.43, г), легко подсчитать, что в этом примере подвижность руки относительно плечевого пояса оценивается 7-ю степенями свободы.

Положение о преодолении избыточных степеней свободы при работе наглядно изображается на кинематической схеме (см. рис. 17.43, а), если момент мышечных сил в каждом суставе разложить на его составляющие по степени свободы (см. 17.43, г). Очевидно, что число этих компонент момента будет равно числу степеней свободы.

Различают две задачи динамики. При решении первой задачи считается, что известны законы движения всех звеньев (обоб­щенные координаты) и определяются суставные моменты и дина­мические нагрузки в суставах. Этот расчет позволяет оценить прочность, жесткость и надежность исследуемой системы. Вторая задача динамики заключается в определении динамических оши­бок — отклонений законов движения от заданных. Известными счита­ются внешние силы и находятся законы движения.

При решении задач динамики необходимо выбрать и обосновать динамическую расчетную схему. Важную роль при их построении играет моделирование воздействий внешних факторов, в том чис­ле трения, материала и др. Затем строят математическую модель, соответствующую динамической расчетной схеме.

При построении динамических расчетных схем тела человека актуальным является определение масс-инерционных характери­стик (МИХ) сегментов тела: масс, моментов инерции, координат центров масс отдельных сегментов (частей) тела. Границы сегмен­тов набирают таким образом, чтобы внутри сегмента отсутство­вала деформация или непроизвольное изменение геометрии масс сегмента. Обычно выделяют следующие сегменты: стопу, голень, бедро, кисть, предплечье, плечо, голову, верхний, средний и ниж­ней отделы туловища. На рис. 17.45 указаны значения моментов

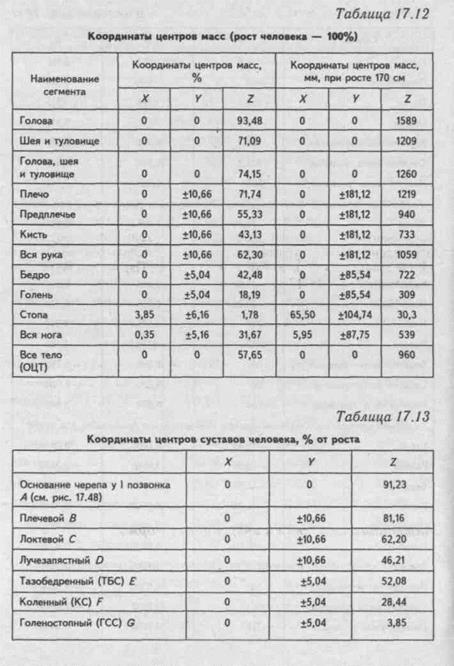
инерции основных сегментов (оси обозначены в соответствии с рис. 2.1); на рис. 17.45 — антропометрические точки, определяющие границы сегментов и координаты центров масс сегментов на их про­дольных осях, в табл. 17.12 — относительные массы сегментов (за 100% принята масса тела).

Оценку масс-инерционных параметров выполняют как прямыми методами (погружение в воду, внезапное освобождение, сечение трупов, компьютерная томография и др.), так и с использованием методов математического и физического моделирования. В послед­ние годы наиболее удобным методом является метод геометричес­кого моделирования.

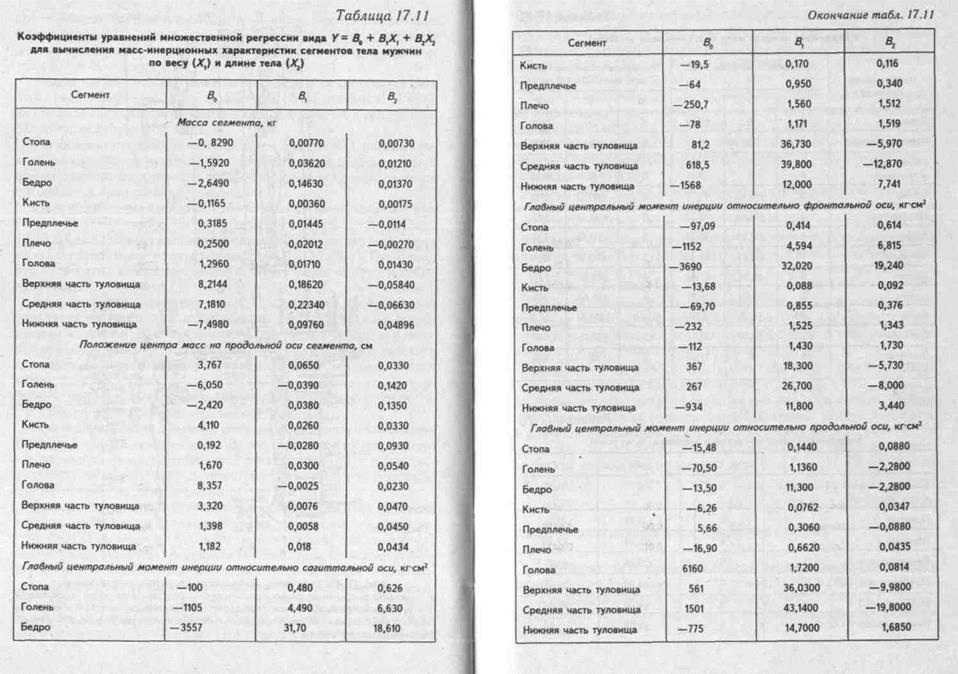
Метод прост, для его выполнения необходимы антропометрические измерения (10 обхватов и 10 длин). Минимум ошибок прогнозируется для МИХ отдельных сегментов за счет введения индивидуальных ко­эффициентов квазиплотности. Кроме этих методов, используют метод определения МИХ по уравнению регрессии, с использованием массы (X_t) и длины тела (X,): Y = В₀ + В_ХХ_Х + BJC_r Параметры регрессии представлены в табл. 17.11.

Антропометрические характеристики определяют геомет­рические размеры тела человека и отдельных его сегментов: это величины, случайным образом измеряющиеся в зависимости от возраста, пола, национальности, рода занятий и т. д.

Основные статические, т. е. измерения при фиксированной позе, размеры тела приведены на рис. 17.46, а, и в табл. 17.8.

Динамические антропометрические характеристики исполь­зуют для оценки объема рабочих движений, зон досягаемости и в других биомеханических и эргономических задачах, в частности при создании антропометрических манекенов. Некоторые дина­мические параметры приведены в табл. 17.11; 17.12; 17.13и на рис. 17.46,6.