Методы теории магнитных цепей
При составлении математических моделей электромагнитов и устройств с постоянными магнитами (далее «магнитные системы») наиболее простыми и в то же время достаточно точными являются методы теории магнитных цепей. Суть этих методов состоит в том, что при расчете магнитных цепей используются уравнения, описывающие законы Ома и Кирхгофа для магнитных цепей, аналогичные тем, которые применяются при расчете электрических цепей. При этом используются аналогии физических параметров, приведенные в таблице П1.1
Таблица П1.1
Аналогии электрических и магнитных параметров,
используемые при анализе магнитных цепей
| № п/п | Параметр электрической цепи | Обозначение | Единица физ. величины | Параметр магнитной цепи | Обозначение | Единица физ. величины |
| Электрический ток | I | А | Магнитный поток | F | Вб | |
| Электро-движущая сила (ЭДС) | E | В | Магнито-движущая сила (МДС) | M | А | |
| Электрическое напряжение | U | В | Магнитное напряжение | Um | А | |
| Электрическое сопротивление | R | Ом | Магнитное сопротивление | Rm | 1/Гн | |
| Электрическая проводимость | L | 1/Ом | Магнитная проводимость | Lm | Гн |
С учетом данных табл. П1.1 уравнения, описывающие основные законы теории магнитных цепей, могут быть записаны в следующем виде.
Уравнение закона Ома для участков магнитной цепи:
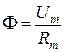, (П1.1)
где F, Um и Rm – соответственно магнитный поток, магнитное напряжение и магнитное сопротивление участка магнитной цепи.
Уравнение первого закона Кирхгофа для узла магнитной цепи:
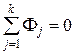, (П1.2)
где Fj – j-й магнитный поток (со своим знаком); k – число ветвей магнитной цепи, сходящихся в данном узле.
Уравнение второго закона Кирхгофа для замкнутого контура магнитной цепи:
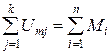, (П1.3)
где Umj – магнитное напряжение на j-м участке замкнутого контура (со своим знаком); k – число участков контура, содержащих магнитное сопротивление; Mi – МДС i-го участка замкнутого контура (со своим знаком);
n – число источников МДС в контуре.
Дата добавления: 2015-07-22; просмотров: 839;