Потери на утечку пара через наружные уплотнения
Часть пара не участвует в процессе на лопатках турбины, т.к. утекает через уплотнения.
Уплотнение наружных концов вала турбины и промежуточных диафрагм осуществляется при помощи лабиринтов.
Цель лабиринтов – дросселирование пара от начального давления Р1 до более низкого Р2. При этом часть пара протекает через лабиринт и не участвует в процессе на лопаточном венце.
В части высокого давления лабиринты предотвращают утечку пара из корпуса турбины. В части низкого давления конденсационных турбин предотвращают проникновение воздуха в турбину и затем в конденсатор. Обычно со стороны низкого давления к лабиринтам подводится пар с давлением выше атмосферного, который частично протекает наружу, а частично в корпус турбины.
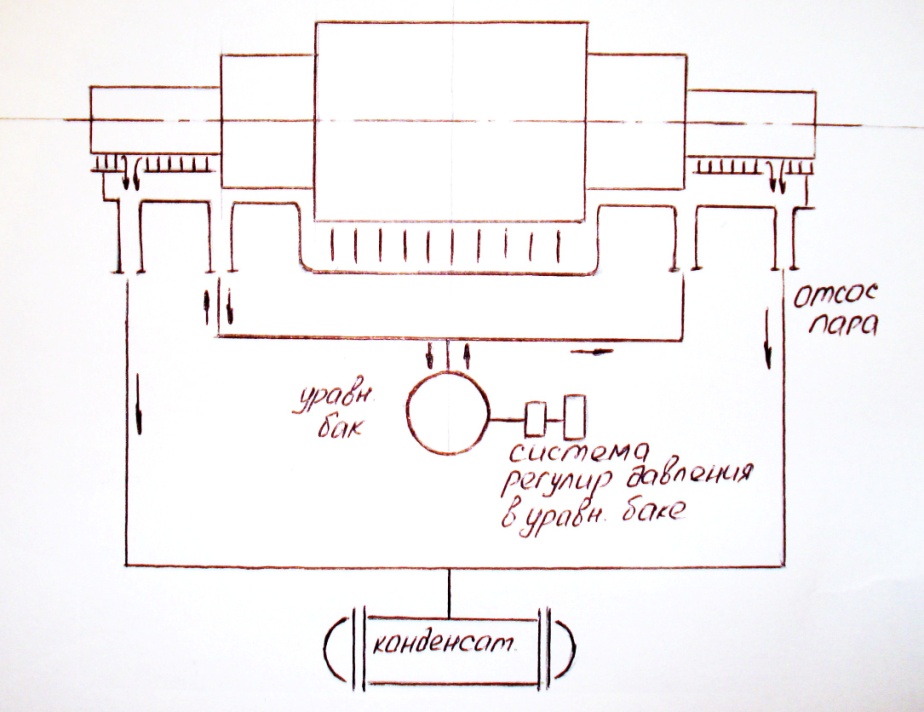
Система укупорки уплотнений.
Лабиринтовые уплотнения имеют множество различных конструкций.
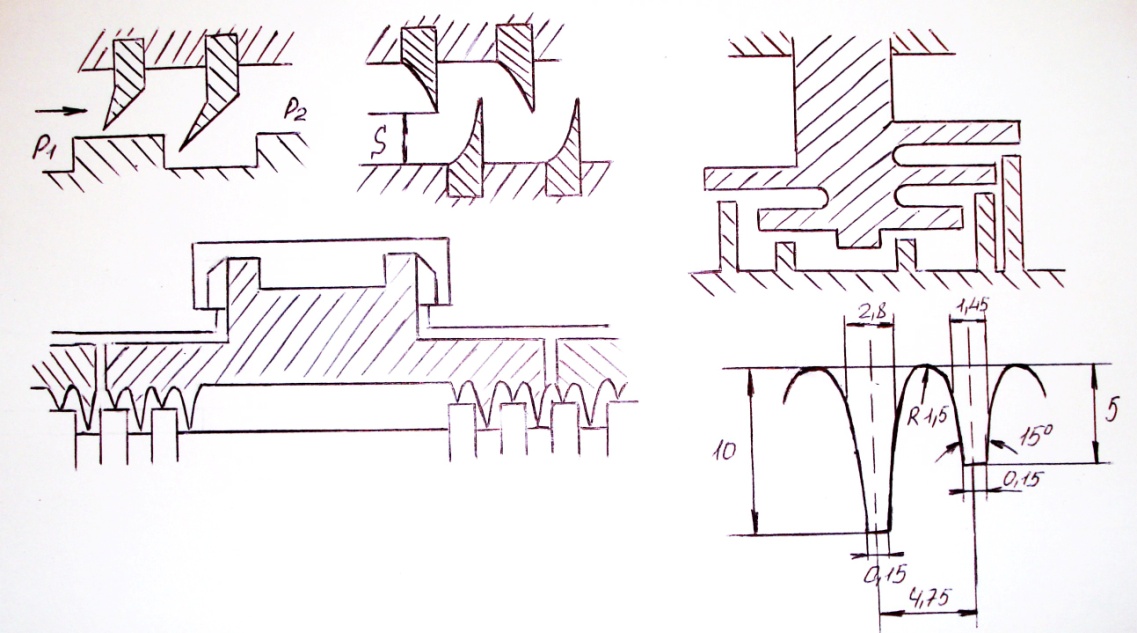
Уплотнение ХТГЗ
Данное уплотнение требует высоких качеств материалов, который при задевании не должен выкрашиваться или «намазываться». ХТГЗ изготовляет из нейзильбера (~ 65% Cu;
14% Ni; 20% Zu; 1% Su).
«Энергомашиностроение» №12 1960г.
Число лабиринтов рассчитывается так, чтобы величина утечки была малой, обычно
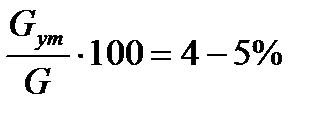
тепловая потеря
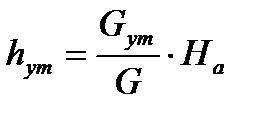 , Дж/кг
, Дж/кг
Величина осевых зазоров 0,15 – 0,35 мм., радиальных 0,5 – 0,6 мм.
Процесс течения пара по лабиринтовому уплотнению показан схематично на рисунках.
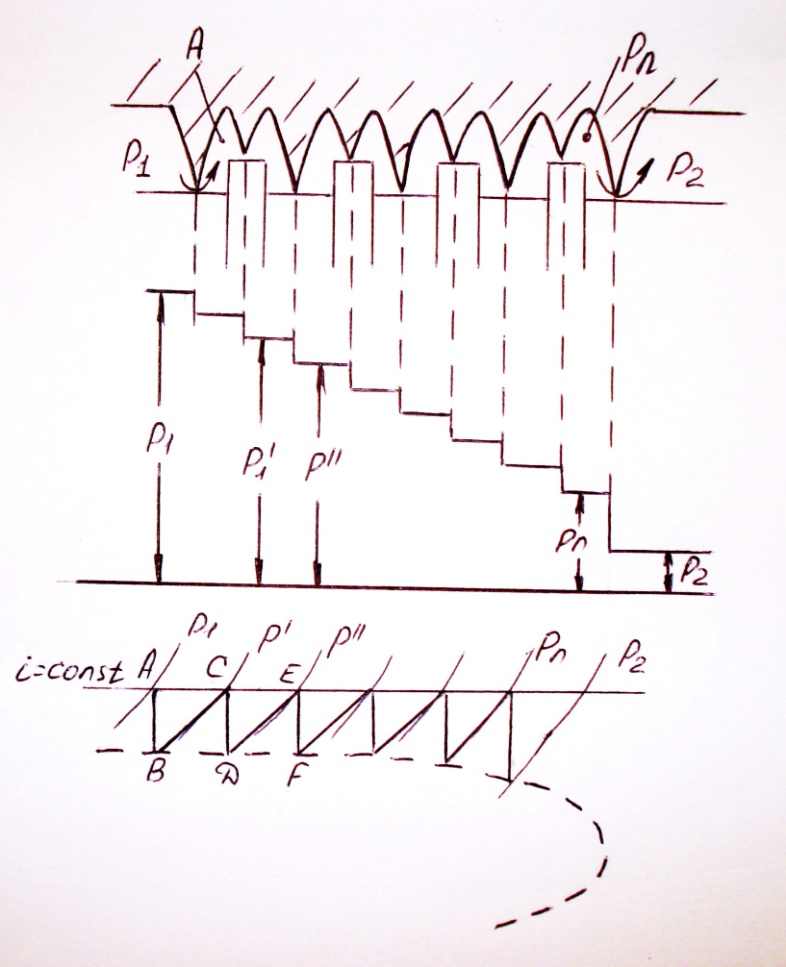
Весь перепад давлений от Р1 внутри корпуса турбины до Р2 – за лабиринтовым уплотнением распределяется между лабиринтовыми камерами, так как показано на рисунке. При прохождении щели давление пара падает, например, от Р1 до Р’, а скорость возрастает до С1. После щели пар со скоростью С1 попадает в объем А, где скорость потока гасится, переходя в тепло и повышая теплосодержание пара да прежнего значения. Этот процесс показан в координатах is на рисунке. Процессу расширения пара в лабиринте соответствует ломаная ABCDEF. При этом точка A, C, E и т.д. лежат на линии i = const. Наивысшая скорость пара возникает в последнем лабиринте.
Для каждой щели справедливо уравнение сплошности
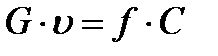 , G - массовый расход кт/сек; υ - удельный объем пара м3/кт.
, G - массовый расход кт/сек; υ - удельный объем пара м3/кт.
Поскольку расход пара или газа через все щели одинаков, то пренебрегая разницей в площадях ------ проходного сечения лабиринтов (т.е. считая все проходные сечения ----- одинаковыми) мы можем написать
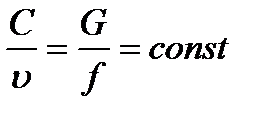 , т.е.
, т.е. 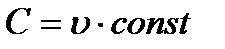
По мере расширения потока в лабиринтах его удельный объем будет возрастать и скорость течения от щели к щели должна увеличиваться, т.е. перепад тепла, срабатываемый в каждой последующей щели, будет больше нежели в предыдущей, что хорошо видно из рисунка. Точки B, D, F лежат на одной кривой, удовлетворяющей 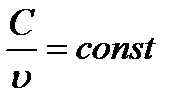 . Эти кривые могут быть построены для различных
. Эти кривые могут быть построены для различных 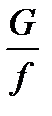 и носят название кривых Фанно.
и носят название кривых Фанно.
Приближенная теория расчета лабиринтового уплотнения разработана профессором Стодола и затем упрощена профессором Уваровым.
I случай: малые перепады давлений в каждой щели
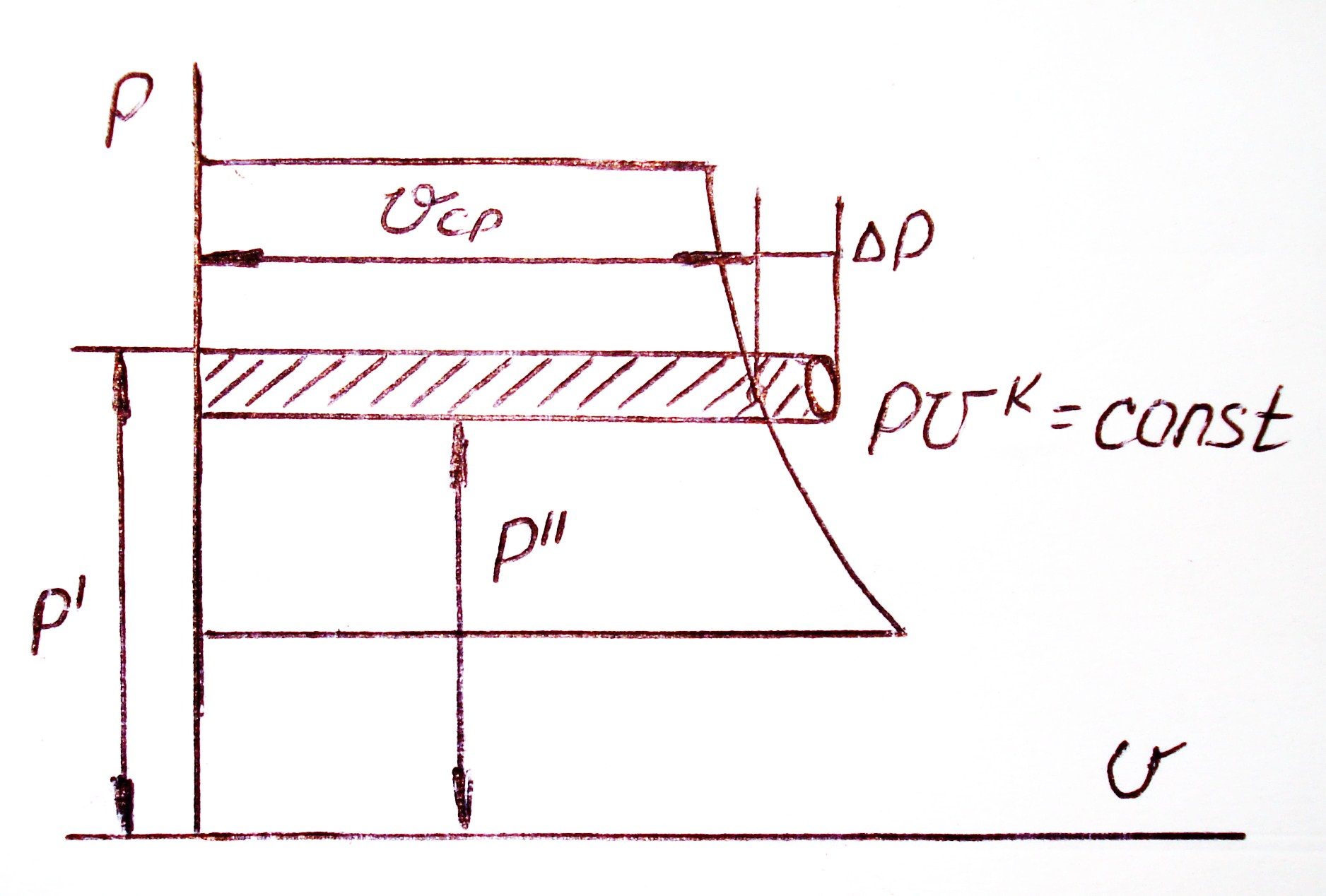
В координатах рυ располагаемая работа при расширении пара в одном лабиринте изображается заштрихованной площадью, заключенной между осью ординат, изобарами Р’ и Р’’ и изоэнтропой рυк = const. При небольших перепадах давления 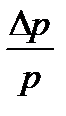 ≤ 0,1 для определения располагаемого теплоперепада (или работы) можно пользоваться приближенной формулой
≤ 0,1 для определения располагаемого теплоперепада (или работы) можно пользоваться приближенной формулой
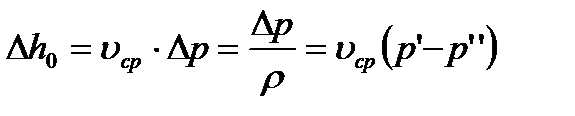
Поскольку при расширении пара при течении через щель или сопло вся располагаемая работа идет на приращение кинетической энергии, то можно написать
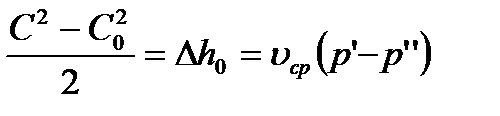
пренебрегая начальной скоростью C0 (оно гасится перед щелью полностью) получим
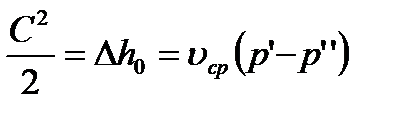
При малом перепаде давлений скорость пара в лабиринтовой щели
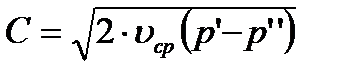 (1)
(1)
и расход газа или пара
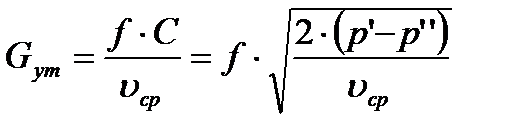 (2)
(2)
Пар в щели лабиринта дросселируется и процесс происходит при i = const, а, следовательно
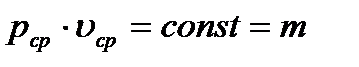
В выше приведенных формулах удельный объем υ должен относиться к среднему давлению
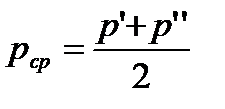
Тогда
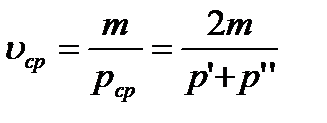
Подставляя υср в уравнение (2) имеем
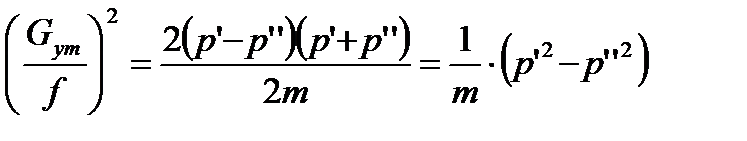
или
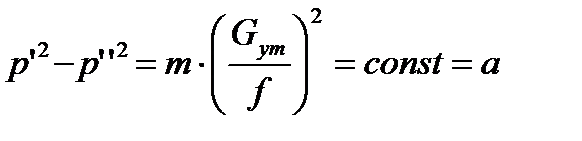 (3)
(3)
Уравнение (3) справедливо для любой щели лабиринта:
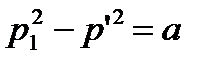 - для первой щели
- для первой щели
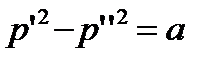 - для второй щели
- для второй щели
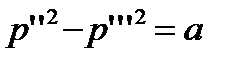 - для третьей щели
- для третьей щели
………………………………
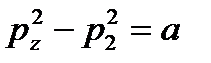 - для последней щели
- для последней щели
Складывая z таких уравнений, получим
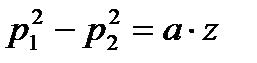 или
или 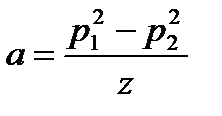
Подставляя в формулу (3) получим
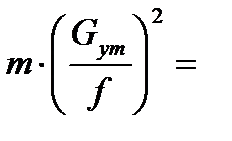
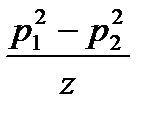 или
или 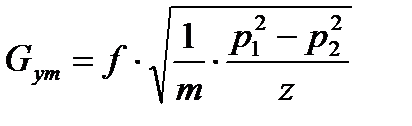
Замечая, что 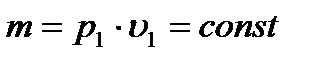 можно написать
можно написать
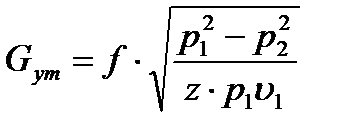 , кг/сек (4)
, кг/сек (4)
Формула (4) пригодна для случая, когда в лабиринте не возникает критической скорости (большое число лабиринтов), т.е. когда
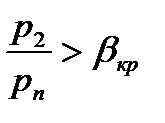 , где Рn - давление в последнем лабиринте.
, где Рn - давление в последнем лабиринте.
II случай:
Если 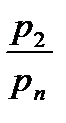 ≤
≤ 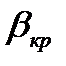 , то расход газа или пара через последнюю щель уплотнения, в которой возникает критическая скорость, может быть подсчитан по формуле для перегретого пара
, то расход газа или пара через последнюю щель уплотнения, в которой возникает критическая скорость, может быть подсчитан по формуле для перегретого пара
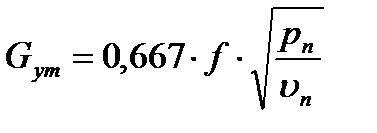 (5)
(5)
где Рn - давление перед последней щелью.
Расход через остальные z-1 щели определяется уравнением (4) с заменой Р2 на Рn.
Т.к. расход через все щели одинаков, то
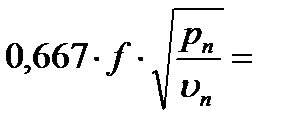
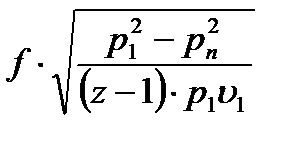
Учитывая, что 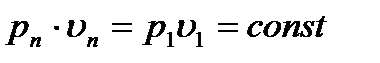 и подставляя
и подставляя 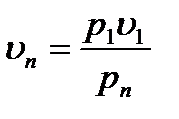 в левую часть этого уравнения и сокращая обе части на f и
в левую часть этого уравнения и сокращая обе части на f и 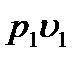 , получим
, получим
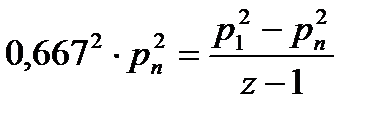
или
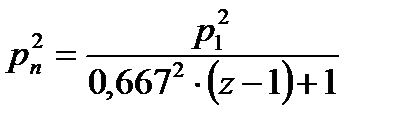 (6)
(6)
или
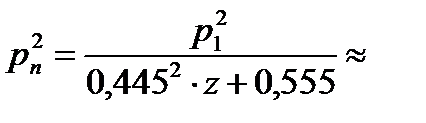
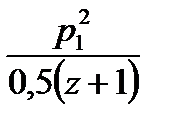 (6а)
(6а)
Тогда расход на утечку пара будет зависеть от Рn
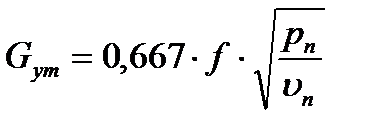 или умножая на Рn
или умножая на Рn
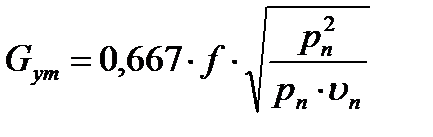
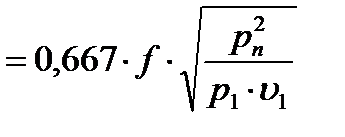
подставляя сюда Р2n из уравнения (6) получим
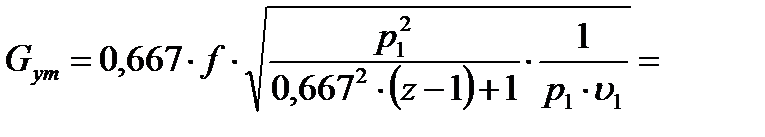
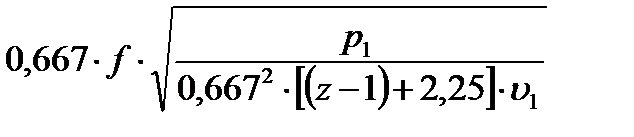
откуда
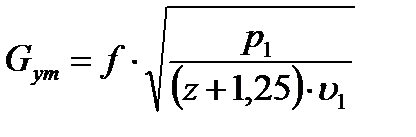 (7)
(7)
где P1 в [Н/м2]
Таким образом, для расчета утечек служат две формулы (4) и (7). Первая применяется в том случае, если отношение 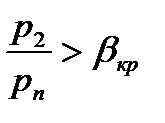 . Вторая формула (7) в том случае, если отношение
. Вторая формула (7) в том случае, если отношение
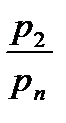 ≤
≤ 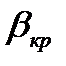 .
.
Критическое значение Р2 = Ркр за последним рассчитываемым лабиринтом найдем, используя уравнение (6а)
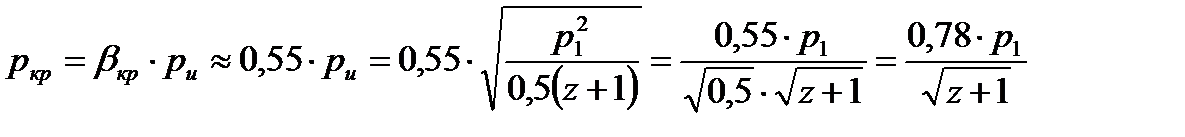 (8)
(8)
Если имеющееся противодавление Р2 > Ркр, то надо применять уравнение (4), если Р2 < Ркр , то надо применять уравнение (7).
Утечка через наружные уплотнения вычитается из общего количества пара, работающего в турбине
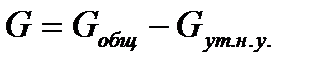
Дата добавления: 2015-07-22; просмотров: 1804;
