Структурно-механические свойства аномально-вязких нефтей

Реологические характеристики нефти в значительной степени определяются содержанием в ней смол, асфальтенов, твердого парафина, порфиринов. Асфальтены за счет плохой растворимости в углеводородах представляют собой коллоидные системы. Мицеллы асфальтенов стабилизируются смолами.

При значительном содержании парафина и асфальтенов вязкость нефти зависит от скорости сдвига, т.е. приобретает свойства неньютоновских жидкостей.

Структурно-механические свойства движущихся неньютоновских жидкостей изучает наука – реология.

Как известно, вязкость ньютоновских жидкостей зависит только от температуры и давления и касательное напряжение 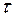, возникающее в движущихся слоях жидкости, пропорционально градиенту скорости :

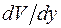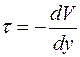. (2.3)

Данное уравнение записывается в форме, аналогичной закону Гука, путем следующих преобразований

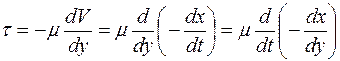, (2.4)

где 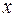– длина в направлении скорости движения 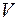; – время.

Величина 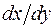характеризует сдвиг 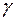слоев (деформацию), и, следовательно, у ньютоновских жидкостей скорость сдвига пропорциональна касательному напряжению и обратно пропорциональна вязкости жидкости

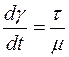. (2.5)

Данное уравнение называют реологическим уравнением.

Вязкость неньютоновской жидкости зависит не только от давления и температуры, но и от скорости деформации сдвига и предыстории состояния жидкости (от времени ее нахождения в спокойном состоянии). Свойства этих жидкостей описываются реологическим уравнением другого вида

. (2.6)

В зависимости от вида функции 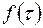эти жидкости разделяются на три вида:

1) бингамовские пластики;

2) псевдопластики;

3) дилатантные жидкости.

Реологические кривые для различных видов жидкостей приведены на рисунке.

Реологическая кривая 1 относится к бингамовским пластикам. В этом случае нефть проявляет свойства пластической жидкости. В состоянии равновесия нефтяная система ведет себя как пластическая жидкость (рис. 3.26) и обладает некоторой пространственной структурой, способной сопротивляться сдвигающему напряжению (τ), пока величи-на его не превысит значение статического напряжения сдвига (τ_о). После достижения некоторой скорости сдвига нефть способна течь как ньютоновская жидкость.

Для определения аномальной вязкости 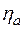таких пластичных тел Ф. Н. Шведовым предложено следующее реологическое уравнение:

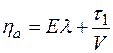, (2.7)

где Е — модуль Юнга;

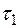— предельное напряжение сдвига;

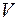— скорость деформации;

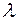– период релаксации (определяет время, необходимое для «рассасывания»

упругих напряжений, возникших в теле при постоянной деформации .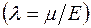

Бингамом аналогичное вязкопластичное течение описывается уравнением:

. (2.8)

Два последних уравнения идентичны и обычно объединяются в одну формулу Шведова – Бингама:

(2.9)

где 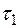динамическое напряжение сдвига;

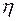– пластическая вязкость, не зависящая от скорости сдвига и равная угловому

коэффициенту линейной части зависимости .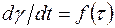

За эффективную вязкость пластичных тел принимается вязкость некоторой ньютоновской жидкости, величина которой

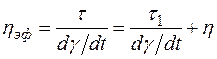. (2.10)

Эффективная вязкость пластичных тел является переменной величиной.

П с е в д о п л а с т и к и (реологическая кривая 2 на рис. III.26) характеризуются отсутствием предела текучести, а также тем, что эффективная их вязкость понижается с увеличением скорости сдвига. Псевдопластиками такие жидкости называют потому, что в определенном интервале напряжений они подчиняются уравнению Шведова — Бингама.

Д и л а т а н т н ы е жидкости (кривая 4) также относятся к телам, у которых отсутствует предел текучести, однако их эффективная вязкость в отличие от псевдопластиков повышается с возрастанием скорости сдвига. Такой тип течения характерен для суспензий с большим содержанием твердой фазы. Предполагается, что в покое жидкость равномерно распределяется между плотно упакованными частицами и при сдвиге с небольшой скоростью жидкость служит смазкой, уменьшающей трение частиц. При больших скоростях сдвига плотная упаковка частиц нарушается, система расширяется и жидкости становится недостаточно для смазки трущихся поверхностей. Действующие напряжения в таком случае должны быть значительно большими.

Движение псевдопластиков и дилатантной жидкости аппроксимируется степенным законом зависимости касательного напряжения и модуля скорости деформации